Question

Задание по геометрии: 1) В прямоугольном равнобедренном треугольнике гипотенуза равна 12 см. Найти катеты этого треугольника.
2) Найти меньшую диагональ ромба, если его сторона равна 13 см, а большая диагональ ромба равна 24 см.

Answer 1

Чертежи смотрите во вложении.

✧Задание №1.✧

В прямоугольном равнобедренном треугольнике гипотенуза равна 12 см. Найти катеты этого треугольника.

Дано :

ΔАВС - равнобедренный и прямоугольный (∠В = 90°, АВ = СВ).

АС = 12 см.

Найти :

АВ = ?

СВ = ?

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы (теорема Пифагора).

Пусть АВ = СВ = х. Тогда АВ² + СВ² = АС²

х² + х² = 12²

2х² = 144

х² = 72

х₁ =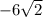 $-6\sqrt{2}$ - не удовлетворяет условию задачи, так как длины отрезков не могут выражаться отрицательными числами.

х₂ =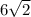 $6\sqrt{2}$ - подходит.

Тогда АВ = СВ = х =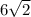 $6\sqrt{2}$ см.

$6\sqrt{2}$ см, $6\sqrt{2}$ см.

✧Задание №2.✧

Найти меньшую диагональ ромба, если его сторона равна 13 см, а большая диагональ ромба равна 24 см.

Дано :

Четырёхугольник ABCD - ромб.

ВС = 13 см, АС = 24 см.

Найти :

BD = ?

В ромбе диагонали точкой пересечения делятся пополам и взаимно перпендикулярны.

Следовательно, АС⊥BD, ВО =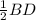 $\frac{1}{2} BD$, CO = 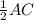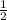$\frac{1}{2} AC$ = $\frac{1}{2}$*24 см = 12 см.

Рассмотрим ΔВОС - прямоугольный (∠ВОС = 90°).

По теореме Пифагора -

ВО² + СО² = ВС²

ВО² = ВС² - СО² = 13² - 12² = 169 - 144 = 25 ⇒ ВО =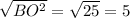 $\sqrt{BO^{2} } =\sqrt{25} =5$ см.

Тогда BD = 2*BO = 2*5 см = 10 см.

10 см.