Question

Урінобедреному трикутнику бічна сторона точкою дотику вписаного кола поділяється на відрізки 4см і 6 см починаючи з вершини основи. довжина кола 6п см. обчислити площу трикутника

Answer 1

Я не понял, откуда идёт деление боковой стороны на орезки 4 и 6, сделал решение, в котором получаются целые значения. Длина окружности тоже, в общем-то лишнее данное, можно решать и без неё. Итак:

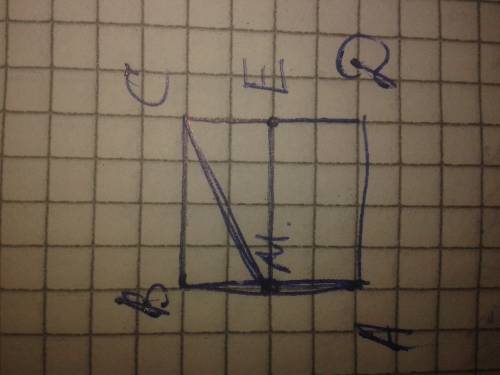
Смотрим рисунок. Поскольку центр вписанной окружности лежит в точке пересечения биссектрис, то угол ЕАО= углу FАО.

В Δ ЕАО и Δ FАО углы Е и F прымые, значит  Δ ЕАО=Δ FАО по четвёртому признаку равенства прямоугольных треугольников (равенство гипотенузы и острого угла).

Значит АF=АЕ=6 см.

Точно так же  Δ DCО=Δ FCО, и DC=FC=6 см

Теперь известны длины сторон ΔАВС:

АВ=ВС=10 см

АС=12 см

Находим площадь ΔАВС, применяя формулу Герона:

$S=\sqrt{p(p-a)(p-b)(p-c)}$,где а, b и с- длины сторон треугольника, р- полупериметр,

$p=\frac{a+b+c}{2}$

$p=\frac{10+10+12}{2}=16$ см

$S=\sqrt{16(16-10)(16-10)(16-12)}=\sqrt{16\cdot6\cdot6\cdot4}=$

$=\sqrt{16}\cdot\sqrt{36}\cdot\sqrt{4}=4\cdot6\cdot2=48$ см²

Можно решить и по другому, с использованием длины окружности:

Из длины окружности находим её радиус:

$L=2\pi$

$\r=\frac{L}{2\pi}=\frac{6\pi}{2\pi}=3$ см

Из ΔВЕО находим ОВ:

$OB=\sqrt{BE^2+EO^2}=\sqrt{4^2+3^2}=\sqrt{16+9}=\sqrt{25}=5$ см

$BF=BO+OF=5+3=8$ см

$S=\frac{AC\cdotBF}{2}=\frac{12\cdot8}{2}=48$ см²

Если допустить, что боковая сторона делится по=другому (АЕ=4 см, ВЕ=6 см), тогда целых значений не получается, поэтому я оставил это решение.

Ну и, как "Лучшее решение" не забудь отметить, ОК?!... ;)))