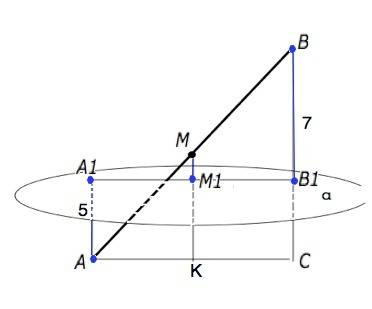
Отрезок АВ пересекает плоскость α, следовательно, т.А и т.В расположены по по разные стороны от плоскости.
Через две параллельные прямые можно провести плоскость, притом только одну. АА1 и ВВ1 лежат в одной плоскости, параллельная им ММ1 лежит в той же плоскости. Эта плоскость пересекает плоскость α по прямой А1В1.
Проведем АС║А1В1 и продолжим ММ1 до пересечения с ней в т.К, а ВВ1 - в точке С.
В параллелограмме АА1В1С стороны СВ1=АА1=5, МК параллельна им и равна 5.
В ∆ АВС прямая МК - средняя линия и равна половине ВС.
ВС=ВВ1+СВ1=12
МК=12:2=6
ММ1=МК-М1К=6-5=1 ( ед. длины)
Объяснение:
АЕ - биссектриса. ⇒ ∠ВАЕ=∠ЕАС=30°:2=15°. ⇒ ∠ВЕА=180°-120°-15°=45°
По т.синусов АВ/sin45°=BE/sin15°.
sin 45°=1/√2; sin 15°=(√3-1)/2√2 (по таблице)⇒ АВ√2=8•2√2/(√3-1) AB=16/(√3-1). Домножив числитель и знаменатель дроби на (√3+1), получим АВ=16(√3+1)/(√3-1)•(√3+1)=8(√3+1).
S(ABC)=AB•BC•sinABC/2 => S(ABC)=[8(√3+1)]²•√3/4=32√3( 2+√3) см²