опустим из тупого угла трапеции высоту на большее основание. получим прямоугольный треугольник с гипотенузой=диагонали трапеции, один из острых углов которого 30° из условия . высота, как катет, противолежащий углу 30°, равна половине диагонали и равна 2 см боковая сторона равна 2√2, отсюда отрезок, который высота отрезала от большего основания, равен 2 см, так как боковая сторона равна диагонали квадрата со стороной 2 см (по формуле диагонали квадрата а√2). так как образовался равнобедренный прямоугольный треугольник, острые углы в нем 45°, и поэтому второй угол при большем основании равен 45°. отсюда тупой угол при меньшем основании равен 180-45=135°.
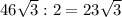 ,
, = 23 * 3 = 69
= 23 * 3 = 69
Ну так треугольник же
1. Прямоугольный
2. Равнобедренный,
Значит его катеты равны по 10, ну площадь
10*10/2=50 (половина квадрата)
Вот и всё!
Да, в условии непонятно сказано о стороне. Я решал "сторона при угле", если "сторона против угла", то решение так же просто.
Значит, задана гипотенуза 10, ну а катеты тогда, конечно, будут 10/sqrt(2), значит площадь
10*10/(2*2) = 25, то есть в 2 раза меньше, чем в первом случае, что совершенно естественно.
Вот теперь совсем всЁ!