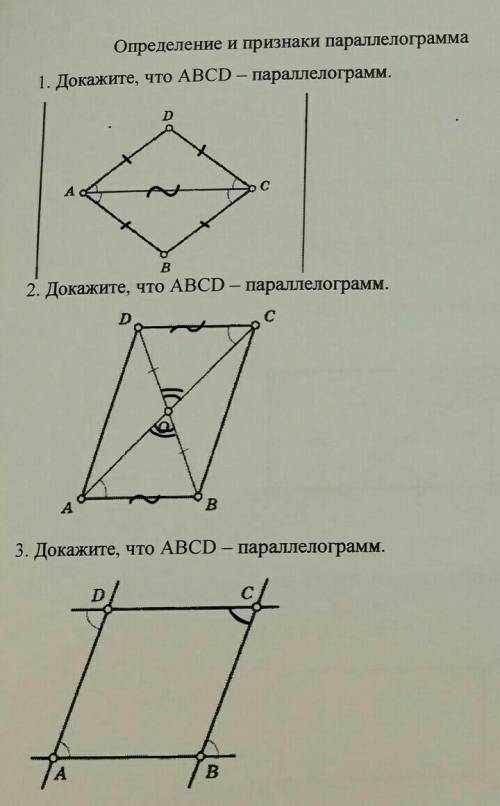
1) Дано: ∠DAC = ∠DCA = ∠CAB = ∠BAC.
Доказать: ABCD - параллелограмм.
Доказательство: Рассмотрим ΔABC и ΔAD.AC - общая сторона, ∠DAC = ∠DCA = ∠CAB = ∠BAC (по условию) ⇒ ΔABC = ΔAD по стороне и двум прилежащим к ней углам.Так как треугольники равны, то и их соответствующие элементы равны. ⇒ AD = BC ; AB = DC. ⇒ABCD - параллелограмм, так как в этом четырёхугольнике противоположные стороны попарно равны.
ответ: что и требовалось доказать.
2) Дано: DO = OB ; ∠OAB = ∠DCO.
Доказать: ABCD - параллелограмм.
Доказательство: Рассмотрим прямые DC и AB при секущей AC.Накрест лежащие углы ∠OAB = ∠DCO (по условию) ⇒ DC║AB.
Рассмотрим ΔAOB и ΔDOC.∠OAB = ∠DCO (по условию) ; DO = OB ; ∠AOB = ∠DOC (вертикальные). ⇒ ΔAOB = ΔDOC по стороне и двум прилежащим к ней углам.Так как треугольники равны, то и их соответствующие элементы равны. ⇒ AB = DC. ⇒ ABCD - параллелограмм, так как в этом четырёхугольнике две противоположные стороны параллельны и равны.
ответ: что и требовалось доказать.
3) Дано: ∠D = ∠A = ∠B.
Доказать: ABCD - параллелограмм.
Доказательство: Рассмотрим прямые DC и AB при секущей AD.Накрест лежащие углы ∠D = ∠A (по условию) ⇒DC║AB.Так как DC║AB, то ∠B = ∠C (как накрест лежащие углы при пересечении параллельных прямых секущей).Теперь рассмотрим прямые AD и BC при секущей DC.Соответственные углы ∠D = ∠C (по выше доказанному) ⇒ AD║BC. ⇒ ABCD - параллелограмм, так как в этом четырёхугольнике противоположные стороны попарно параллельны (по определению).
ответ: что и требовалось доказать.
Объяснение:
Решим данную задачу при уравнения.
Пусть один из смежных углов х градусов, тогда второй из смежных углов 3×х градусов. Нам известно, что сумма градусных мер смежных углов равна 180 градусов. Составляем уравнение:
х + 3 × х = 180;
х × (1 + 3) = 180;
х × 4 = 180 (для того, чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель);
х = 180 : 4;
х = 45 градусов — один из смежных углов;
45 × 3 = 135 градусов — второй из смежных углов.
ответ: 45 и 135 градусов.
Дано:
Равнобедренный ΔАМС
МК - высота ΔАМС, опущенная на основание АС
АС- основание ΔАМС
АМ = СМ = 3,4 АС - боковая сторона ΔАМС
Р = 31,2 см - периметр ΔАМС
Найти:
АС; АМ=СМ; - стороны ΔАМС
Периметр ΔАМС равен
Р = АМ + СМ + АС = 31,2 см
Поскольку АМ = СМ = 3,4 АС, то
3,4АС + 3,4АС + АС = 31,2
7,8 АС = 31,2
АС = 4 (см) - основание ΔАМС
АМ=СМ = 3,4 · 4 = 13,6 (см) - боковая сторона ΔАМС
Высота МК равнобедренного ΔАМС, проведённая к его основанию АС, является его медианой, поэтому отрезок КС равен половине основания АС:
КС = 0,5 АС = 0,5 · 4 = 2 (см)
Основание ΔАМС: АС = 4 см
Боковые стороны ΔАМС: АМ = СМ = 13,6 см
Отрезок КС = 2 см