° ° + 13° =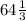 
° °; °
°
° ° ° 
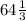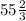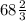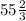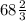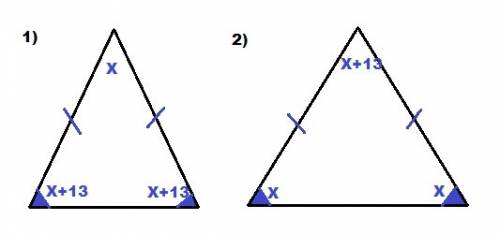
Построение сечения: Назовем искомую плоскость MNK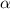 
. Плоскости ABC и A1B1C1 параллельны и пересечены плоскостью 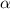, следовательно, линии пересечения параллельны. Значит, 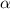пересекает А1В1С1 по прямой КF, параллельной MN. Значит, F - середина А1В1. Осталось соединить KF, FM, MN, NK. Искомое сечение - FKNM.
Доказательство: В треугольнике ABD MN-средняя линия, MN || BD. Т.к MN лежит в плоскости сечения MNK, а BD параллельна прямой MN, лежащей в плоскости сечения, ВD параллельна плоскости MNK, что и требовалось доказать.
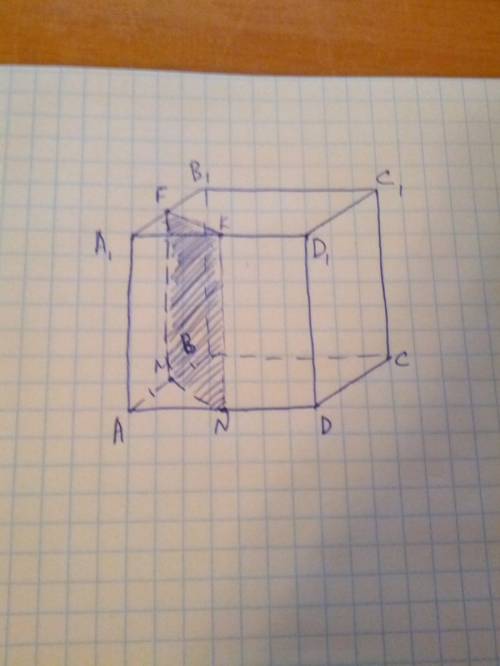
Рассмотрим тр-кА1АС. А1А=6, АС=8; по теореме Пифагора найдем А1С: 36+64=100(10). А1С=10