Объяснение:
При вращении прямоугольника вокруг стороны 8 см получается цилиндр с высотой 8 см и радиусом основания 6 см.
Площадь полной поверхности цилиндра равна сумме площадей боковой поверхности и удвоенной площади основания.
Площадь боковой поверхности - произведение длины окружности основания и высоты цилиндра:
Sбок=L*Н; L=2πr=2π*6=12π, Н=8, Sбок=12π*8=96π см²;
Sосн=πr²=π*6²=36π; 2Sосн=72π см²;
Sпол.пов.=Sбок+2Sосн=96π+72π=168π см².
Объем цилиндра - произведение площади основания на высоту цилиндра.
Vцил.=Sосн*Н=36π*8=288π см³.
А₁А₂ = 2 см
Объяснение:
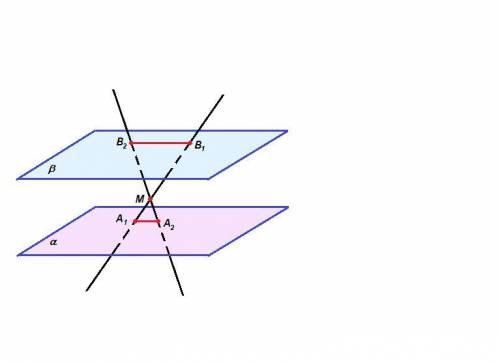
Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны.
Пересекающиеся прямые А₁В₁ и А₂В₂ задают плоскость, которая пересекает плоскости α и β по прямым А₁А₂ и В₁В₂, значит
А₁А₂ ║ В₁В₂.
Тогда ∠МВ₁В₂ = ∠МА₁А₂ как накрест лежащие при пересечении параллельных прямых А₁А₂ и В₁В₂ секущей А₁В₁,
∠В₁МВ₂ = ∠А₁МА₂ как вертикальные, значит
ΔВ₁МВ₂ подобен ΔА₁МА₂ по двум углам.
МВ₂ = А₂В₂ - МА₂ = 10 - 4 = 6 см
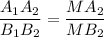
Пусть А₁А₂ = х, тогда В₁В₂ = х + 1,
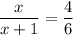
6x = 4(x + 1)
6x = 4x + 4
2x = 4
x = 2
А₁А₂ = 2 см
ΔABC - прямоугольный, ∠С = 90°, ∠А = 60°, BC = 17√3; AB = 34
Сумма острых углов прямоугольного треугольника равна 90°. ⇒
∠B = 90° - ∠A = 90° - 60° = 30°
Катет, лежащий напротив угла 30°, равен половине гипотенузы. ⇒
AC = AB : 2 = 34 : 2 = 17
Площадь прямоугольного треугольника равна половине произведения катетов.
ответ : 144,5√3 ≈ 250,28 кв. ед.