Боковая сторона равнобедренного треугольника равна 10 см, а его основание 12 см. Найдите его площадь.
Биссектриса угла А параллелограмма ABCD делит сторону ВС на отрезки ВК и КС, равные соответственно 8 см и 4 см. Найдите периметр параллелограмма.
В трапеции ABCD углы А и В прямые. Диагональ АС — биссектриса угла А и равна 6 см. Найдите площадь трапеции, если угол CDA равен 60°.
В окружности проведены две хорды АВ и CD, пересекающиеся в точке К, КС = 6 см, АК = 8 см, ВК + DK = 16 см. Найдите длины ВК и DK.
Квадрат со стороной 8 см описан около окружности. Найдите площадь прямоугольного треугольника с острым углом 30°, вписанного в данную окружность.
Проведем перпендикуляр SO к плоскости основания и перпендикуляры SK, SM и SN к сторонам ΔABC. Тогда по теореме о трех перпендикулярах OK ⊥ BC, ОМ ⊥ АС и ON ⊥ AB.
Тогда, ∠SKO = ∠SMO = ∠SNO = 45° — как линейные углы данных двугранных углов.
А следовательно, прямоугольные треугольники SKO, SMO и SNO равны по катету и острому углу.
Так что OK=OM=ON, то есть точка О является центром окружности, вписанной в ΔАВС.
Выразим площадь прямоугольника АВС:
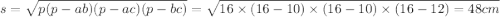
С другой стороны можно S=p×r
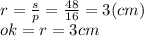
Так как в прямоугольном треугольнике SOK острый угол равен 45°, то ΔSOK является равнобедренным и SO=OK=3 см.
ответ: 3 см.
Трикутник АВС, АВ=9, ВС=24, кутВ=60
АС = корінь(АВ в квадраті + ВС в квадраті - 2 х АВ х ВС х cosB) =
=корінь (81 + 576 - 2 х 9 х 24 х 1/2) =21
Периметр = 9+24+21=54, полупериметр =54/2=27
площа = корінь (p x (p-a) x (p-b) x (p-c)) =корінь (27 х (27-9) х (27-24) х (27-21) =
=корінь 8748=93,5
або
площа= 1/2АВ х ВС х sin60=1/2 х 9 х 24 х корінь3/2 = 54 х корінь3