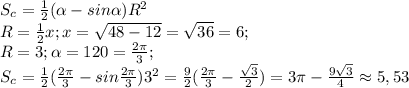
Объяснение:
1)АМ - гипотеза, ВМ-катет против угла 30*,тогда
ВМ=1/2 ВМ=26:2=13
2)<А=90-60=30*,тогда ВМ-катет против угла 30*,ВМ=30:2=15
5)∆АВС - равносторонний, все углы равны и высота является биссектрисой, <МАВ=30*
Расстояние от М до АВ - это перпендикуляр МК к стороне АВ и в ∆МКА МК является катетом против угла 30* и МК=МА:2=8:2=4
6) кратчайшее расстояние от М до АВ - это высота из вершины М.
∆АВМ прямоугольный, равнобедренный и высота МН является медианой. Тогда по свойству медианы прямоугольного треугольника МН=8:2=4
Катет как диаметр равен 4V3 * cos 30 = 4*V3*(V3/2) = 6, r = 3 см.
Отсекаемая часть круга является сегментом с углом 120 градусов. Дуга проти вписанного угла в 30 равна 2*30 = 60 градусов. 180 - 60 = 120 градусов.
Площадь сегмента равна площади сектора (S1) минус площадь треугольника.(S2)
S1 = пи *r^2 * n/360 = пи * (3^2) * 120/360 = 3 *пи
h = r*sin 30 = 3 * 0,5 = 1,5 = 3/2
a = 2*(r*cos 30) = 2 * 3 * (V3/2) = 3V3
S2 = 1/2 * (3V3) * 3/2 = 9V3 / 4
S = 3 *пи - 9V3 / 4 =(12пи - 9V3) / 4 = 5,5277.