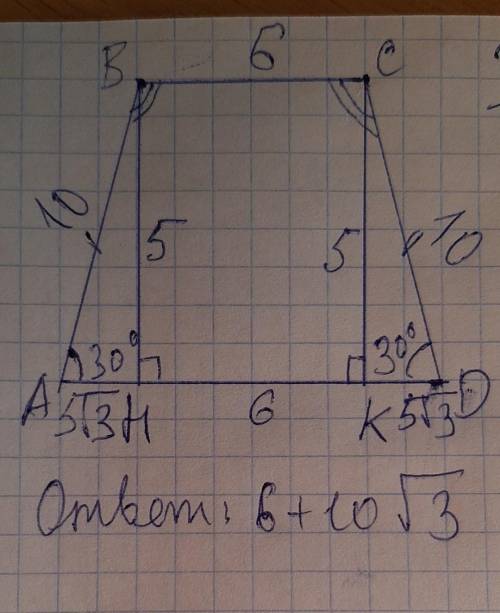
Решение: Проведём высоту СК.
Значит, BHKC прямоугольник, тогда ВС=HK=6 , BH=CK=5.
В треугольнике АВН угол АНВ= 90°, значит треугольник АВН - прямоугольный, т.к. угол А=30° и катет ВН=5, то гипотенуза АВ= 10 ( т.к. в прямоугольном треугольнике катет лежащий против угла в 30° равен половине гипотенузы).
Т.к. АВСD - равнобедеренная трапеция, то угол А = углу D = 30°.
Значит треугольник АВН= треугольнику СКD (по гипотенузе и острому углу)
Треугольнике АВН - прямоуольный:
По теореме Пифагора:
АН² + ВН²= АВ²
АН² = АВ² - ВН²
АН² = 100 - 25 = 75
АН = корень в квадрате из 75 = 5 корней из трёх
АН = КD = 5 корней из трёх
АD = 6 + 5 корней из трёз + 5 корней из трёх = 6 + 10 корней из трёх.
ответ: 6 + 10 корней из трёх.
Дано: ABCD - равнобедренная трапеция угол BAD=45° BO - высота, BO=5 BC=6 см
Найти: ADРешение:
1)ABCD - равнобедренная трапеция(по условию). Отсюда следует, что углы при основании AD равны, т.е. угол BAD=CDA=45°2) После того, как провели высоту BO, образовался прямоугольный треугольник AOB. Если угол BAD = 45°, значит, и второй угол ABO = 45° (180-90-45). Отсюда следует, что треугольник AOB - равнобедренный. Значит, BO=AO=5 см.3) Аналогично находим HD, который будет равняться 5 см.4) BC=OH=6 см(противоположные стороны прямоугольника)5) AD=AO+OH+HDAD=5+6+5=16 см. ВУОЛЯ! ответ: AD=16 см.