ответ: √(x² + y²)
Объяснение:
Расстояние между двумя точками -- это отрезок, соединяющий эти точки.
Воспользуемся формулой нахождения расстояния между двумя точками.
Пусть А(a₁; a₂), B(b₁, b₂), тогда
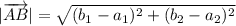
В нашем случае даны точки O(0; 0) и M(x; y). Подставим их координаты в формулу:
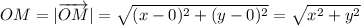
Воспользуемся координатной плоскость и теоремой Пифагора.
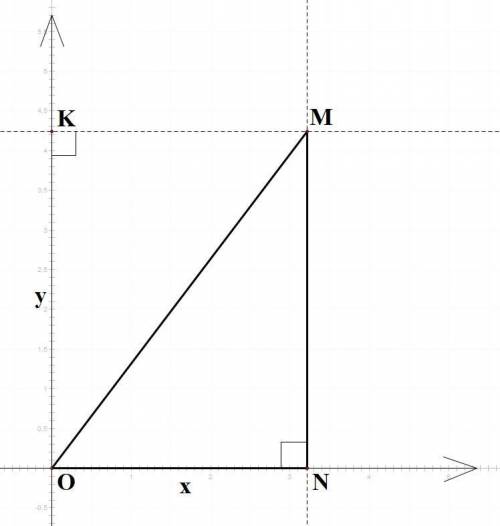
Изобразим на координатной плоскости точки O(0; 0) и M(x; y). Соединим их. Затем опустим перпендикуляры от точки М на ось ОХ и OY, обозначим получившиеся точки N(x; 0) и K(0; y).
(координатная плоскость во вложениях)
Получаем следующее: длина отрезка OK равна y - 0 = y, ON = x.
Также MN = OK = y
Рассмотрим ΔMNO. Он прямоугольный. Применим к нему теорему Пифагора и выразим гипотенузу OM:
а) чему равны радиус окружности и координаты ее центра?
Хо = 3, Уо = -5, R = √25 = 5.
б) докажите что точки А и В лежат на окружности, если А(7; -2), а Б(0; -1).
Надо подставить координаты точек в уравнение окружности:
(7-3)² + (5-2)² = 16 + 9 = 25,
(0-3)² + (-1+5)² = 9 + 16 = 25.
Да, точки лежат на окружности.
2). Вычислите длину хорды АВ из задачи номер 1 ( 1 задание). А(7; -2), Б(0; -1).
Надо подставить координаты точек в уравнение окружности.
L = √(0-7)² + (-1+2)²) = √(49 + 1) = √50 = 5√2 ≈ 7,071068.
3) Пользуясь таблицами, вычислите tg 128 градусов.
128° = 2,234021 радиан, это вторая четверть.
tg 128° = -1,27994.
4) В треугольнике АВС А( -6;4 ), В ( 1;2), С(4;0) проведена медиана ВD. Составьте уравнение прямой, содержащей эту медиану.Находим координаты точки D как середины АС:
D((-6+4)/2=-1; (4+0)/2=2) = (-1; 2).
Уравнение ВD:
ВD: (х-1)/(-1-1) = (у-2)/(2-2),
(х-1)/(-2) = (у-2)/0
у = 2 горизонтальная линия (координаты по у совпадают).