ответ: 8 см²
Объяснение:
КАК решают такие задачи.
Часто подобные задачи решаются вычитания ( или сложения ) площади фигур, образованных клетками. Чертят прямоугольник, который описывает данную фигуру. Вычисляют его площадь, затем площадь "лишних"фигур ( обычно это треугольники) и вычитают. Остается искомая площадь . Или делят данную фигуру на части, у которых удобно найти площадь, и затем складывают.
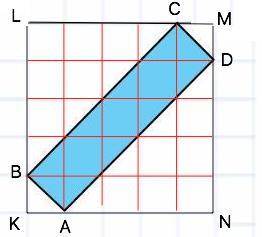
Обозначим прямоугольник АВСD, опишем около него прямоугольник KLMN. (см. вложение).
S(KLMN)=KL•LM=5•5=25 см²
∆BLC=∆AND по равным катетам.
Их общая площадь Ѕ₁=4•4=16 см²
∆BKA=∆CMD по равным катетам. Их общая площадь
Ѕ₂=1•1=1 см²⇒
Ѕ (ABCD)=S (KLMN)- 16-1=8 см²
----------
Другой
Из ∆ (BLC) по т.Пифагора найдем длину ВС=√(4²+4²)=4√2 см.
Из ∆ (ВКС) по т.Пифагора найдем ширину АВ=√(1²+1²)=√2 см
Площадь прямоугольника равна произведению его длины на ширину:
S(ABCD)=ВС•АВ=4√2•√2=8 см²
Рассмотрим треугольники АКС и СМА
Оба они - прямоугольные, имеют общую гипотенузу АС и равные острые углы:
∠А=∠С , т.к. треугольник АВС - равнобедренный и углы при основании АС равны.
Прямоугольные треугольники. в которых равны гипотенуза и острый угол - равны.
Из равенства этих треугольников следует, что
равны и треугольники АКМ и СКМ.
В этих треугольниках равны три стороны.
АМ=КС, АК=СМ, а КМ - общая.
Следовательно, углы КСМ=МАК
Но так как ∠А=∠С, то ∠ А - ∠МАК= ∠С- ∠КСМ.
Мы доказали равенсто углов КСА= МАС
Треугольники АОС и КОМ равнобедренные и подобны,
так как имеют равные стороны КО=ОМ, ОС=ОА, ∠ КОМ=∠АОС как вертикальные, и отсюда углы при основаниях этих треугольников равны ( 180 - ∠АОС):2.
Из подобия равнобедренных треугольников следует, что углы МКС=КСА и КМА=МАС.
Но эти углы - накрестлежащие при КМ и АС и секущих КС и МА.
Следовательно, КМ||АС, что и требовалось доказать.