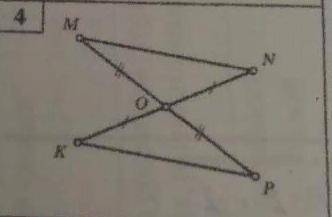
1) 1. рассмотрим АДС-прямоугольный (АД-высота) АД=24см ДС=18см . по тПифагора СА=sqrt24^2+18^2=30cm
2. из соотношения сторон и высоты к гипотенузе прямоугольного треугольника имеем
АС^2=CD*CB CB=AC^2 / CD CB=30^2 / 18= 50cm ДВ=50-18=32см
АВ^2 =DB*CB AB^2=50*32=1600cm^2 AB=40cm
можно было проще : египетский треугольник , соотношение сторон 3:4:5
у АВС АС=30см СВ=50см АС:АВ:СВ =3:4:5=30 :40:50 АВ= 40см
3. сos A -?????? cos90* =0
cosCBA= BA /BC cosBCA=CA/BC cosBAD=BD / BA cosDAC=DA/CA =24 /30=4/5
подставь длинну катета и гипотенузы и вычисли
2) АВСД- трапеция угА=угВ=90*, ВС=3см, СД=4см угВСД=150*
1)проведем СН-высота угВСН=СНА=90* угНСД=150*-90*=60* АН=3см
2)рассмотрим треугольник НСД-прямоугольный угСНД=90* угНСД=60* значт угНДС=30*
напротив угла 30* лежит сторона = 1/2 гипотенузы , отсюда СН=1/2СД =2см
по т Пифагора НД=sqrt (4^2-2^2)=2sqrt3 (2 корня из3)
3) Sтрап =( (a+b) /2 ) * h
S(ABCD) = (3+3+2sqrt3) / 2) *2 =(6+2sqrt3) cm^2
3) Sпрямоуг= а*в
пусть а=АД в=СД
рассмотримАСД-прямоугольный угД=90* САД=37* cos37*= a /c sin37*=b/c
a=3 cos37* b=3 sin37*
S= 3 cos37* * 3 sin37* = 9 * 1/2 sin(37*2)= 4.5 sin74*
Рассмотрим попарно равные треугольники ΔАОN=ΔBОN , они равны по катету /ВО=АО/ и общей гипотенузе ОN,
ΔАОM=ΔCОM, они равны по катету /СО=АО/ и общей гипотенузе ОМ, ΔBОL=ΔCОL, они равны по катету /СО=ВО/ и общей гипотенузе ОL, из равенства этих треугольников следует равенство соответствующих углов ,∠ АОN=∠BОN; ∠BОL=∠CОL; ∠АОМ=∠CОL.
По условию ∠NMO=40°; ∠MAO=90°⇒∠AOM=180°-90°-40°=50°, тогда ∠АОС=2*50°=100°;
Аналогично, ∠LNO=42° ∠NBO=90°⇒∠NOB=180°-90°-42°=48°⇒∠BOA=2*48°=96°
Т.к. сумма всех углов при вершине О равна 360°, то на оставшийся ∠ВОС приходится 360°-100°-96°=164°
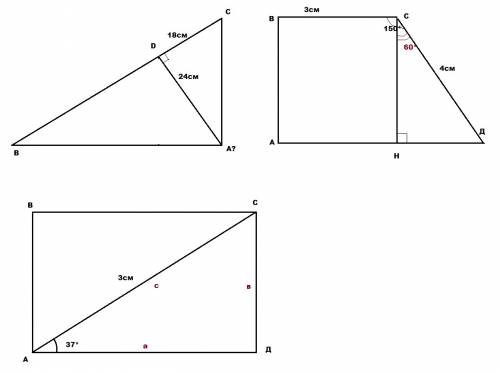
1) Рассмотрим треугольники MNO и KOP:
1) MO=OP ( по условию )
2) KO=ON ( по условию )
3) угол MON = углу KOP ( по свойству вертикальных углов)
из всего этого следует, что треугольники MON=KOP.
из этого следует, что углы NMO=OPK ( как соответственно равные элементы ).
2) MN || KP при секущей MP ( накрест-лежащие ( н/л ) углы NMO и OPK = по признаку о параллельных прямых с н/л углами )
ч.т.д.