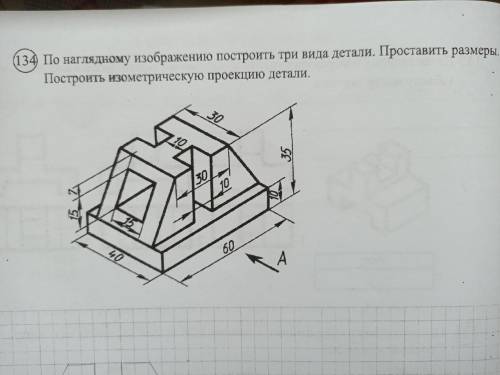
Дано: ΔАВС - равнобедренный, АК = КВ = ВМ = МС (т. К и М - середины боковых сорон АВ и СВ соответственно), ВD - медиана.
Доказать: ΔBKD = ΔBMD.
Доказательство: есть два треугольника BKD и BMD, у которых сторона BD - общая. стороны KB и BM - равны, т.к. ΔABC - равнобедренный, а точки K и M - середины сторон АВ и СВ соответственно. Т.к. BD - медиана равнобедренного ΔABC, то ∠KBD = ∠DBM. Следовательно, по первому признаку равенства треугольников (если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны), треугольники BKD и BMD равны, т.к. KB = BM, BD - общая сторона, ∠KBD = ∠DBM.
Чтд.
См. Объяснение
Объяснение:
Три проекции - в прикреплении.
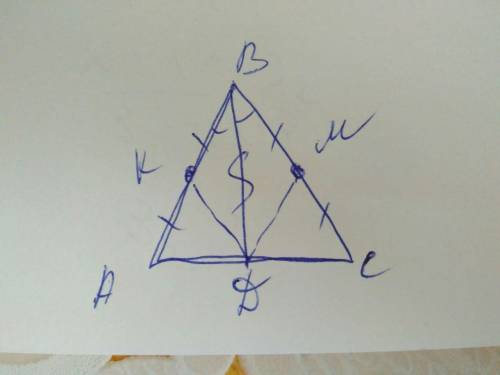
Окно 15х15 - очевидно, сквозной паз, поэтому на виде спереди видно, как он рвёт перемычку, от которой остаётся сверху 7 мм и снизу 3 мм.
На виде спереди и на виде сверху паз обозначен пунктиром.
Тонкие линии - вс
Чтобы перенести размеры окон с вида спереди на вид сверху, необходимо:
- наверху дать горизонтальные линии (на расстоянии 7 мм и 22 мм от верха), до пересечения этих линий с наклонными;
- затем к точкам пересечения приложить линейку и провести линии на виде сверху.