Рисунок во вложении.
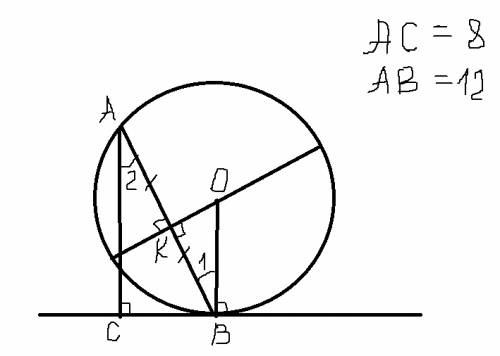
Назовем хорду АВ. Через точку В проведем касательную, из точки А проведем перепндикуляр АС к касательной-это и будет расстоянием от А до касательной. Получили прямоугольный треугольник АВС.
Теперь проведем диаметр окружности перпедикулярно хорде АВ. Он будет делить эту хорду пополам. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею дуги пополам. Точку пересечения хорды и диаметра назовем К .
Проведем радиус ОВ. Так как ОВ перпендикулярен касательной и АС перпендикулярен касательной, то ОВ//АС. Углы 1 и 2 накрест лежащие, значит они равны.
Рассмотрим треугольники АВС и ВОК: они прямоугольные и имеют по равному острому углу, значит они подобны. Из подобия следует, что ОВ:АВ=АС:ВК => ОВ:12=6:8 => ОВ=9
ответ: 9см.
ответ:2.5.3 в прямоугольном треугольнике cosA = sinB или cosB=sinA. у нас есть Cos A 173/371. значит sinB будет 173/371
2.5.4 Синус - отношение противолежащего катета к гипотенузе. То получаем, что катет BC=4√11, а гипотенуза = 15; По т. Пифагора найдем катет AC= √225-176=7
то sinB=7/15
2.5.5 Косинус-отношение прилежащего катета на гипотенузу, косинус угла А равен √91\10, значит прилежащий катет, т.е АС=√91, а гипотенуза=10.
По теореме Пифагора находим катет ВС:
ВС²=ВА²-СА²
ВС²=100-91=9
ВС=3
Косинус-отношение прилежащего катета на гипотенузу, значит косинусом угла В будет служить отношение ВС\ВА=3\10
ответ: 0,3
2.5.6 tg A = sin A/ cos A
Применим основное тригонометрическое тождество:
sin A=√(1-cos²A)=√(1-(√2/4)²)= √(1-2/16)=√(1-1/8)=√(7/8)
Тогда tg A = √(7/8):(√2/4)= √(7/8)·4/√2=4·√(7/16)=4·¼·√7=√7.
ответ: √7.
2.5.7 sina=3(√10)/(√10)²=3/√10
cosa=√(1-sin²x)=√(1-9/10)=√(1/10)=1/√10
tga=sina/cosa=(3/√10)/(1/√10)=(3/√10)*√10=3
вычислаем во всех страны прямоугольника 3 см + 3 см = 6 см
Объяснение: