Дано:АВСD-трапеция(АD-ниж.осн-е),АD=36 см,АВ=СД=25 см,АС=29 см.
Найти:SABCD
Решение:
1)проведём высоту СС1=h.Пусть ВС=х см.С1D=(АD-ВС)/2=(36-х)/2
2)рассмотрим п/у тр-к АСС1:h²=AC²-AC1²=>h²=29²-((36-x)/2)+x)²
3)рассмотрим п/у тр-к СС1D:h²=25²-C1D²=>h²=25²-((36-x)/2)²
29²-(36+x)²/4=25²-(36-x)²/4
(36-x)²/4-(36+x)²/4=25²-29²
...
36x=216
x=6
BC=6 см=>h²=25²-((36-6)/2)²=20 (см).
4)SАВСD=(6+36)*20/2=420(кв.см).
Привет! Хочешь научиться списывать ответы в РЭШ нажатием одной кнопки? При этом чтобы все не слетало и не приходилось заново выполнять утомительные манипуляции с различными полурабочими скриптами? Тогда залетай к нам в телегу https://t.me/reshsell_bot!
Объяснение:
Привет! Хочешь научиться списывать ответы в РЭШ нажатием одной кнопки? При этом чтобы все не слетало и не приходилось заново выполнять утомительные манипуляции с различными полурабочими скриптами? Тогда залетай к нам в телегу https://t.me/reshsell_bot!
ответ: 7,5 см
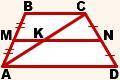
Объяснение:Дано: ABCD — трапеция,
AD∥ BC, MN — средняя линия,
MN∩AC=K, BC=8см, AD=15 см
Найти: MK, KN
Решение: 1) Рассмотрим треугольник ACD.
СN=DN и KN ∥ AD (так как по условию MN — средняя линия трапеции).
Следовательно, по теореме Фалеса, AK=KC.
Значит, KN — средняя линия треугольника ACD.⇒ KN=AD/2=15:2=7,5 см
2) Рассмотрим треугольник ABC.
АМ=MB (так как MN- средняя линия трапеции), AK=KC (по доказанному). Следовательно, MK — средняя линия треугольника ABC,⇒ МК=ВС/2=8:2=4 см.
KN>MK ⇒ ответ: 7,5 см
Трапеция АВСД, АД=36, АВ=СД=25, АС=29
проводим высоты ВН=СК на АД, треугольники АВН=треугольнику КСД , по гипотенузе АВ=СД и острому углу уголА=уголД, АН=КД = а, АК=36-а
треугольник КСД , СК в квадрате = СД в квадрате - КД в квадрате =625 - а в квадрате
треугольник АСК прямоугольный, СК в квадрате = АС в квадрате - АК в квадрате =
=841 - (36-а) в квадрате
625 - а в квадрате = 841 -1296 +72а - а в квадрате, 72а=1080, а=15 =КД=АН
СК=ВН=корень (СД в квадрате-КД в квадрате) = корень(625-225)=20
НК=ВС=АД-АН-КД=36-15-15=6
площадь=(ВС+АД)/2 х СК = (6+36) /2 х 20=420