Пересечение 6 -2.
Объяснение:
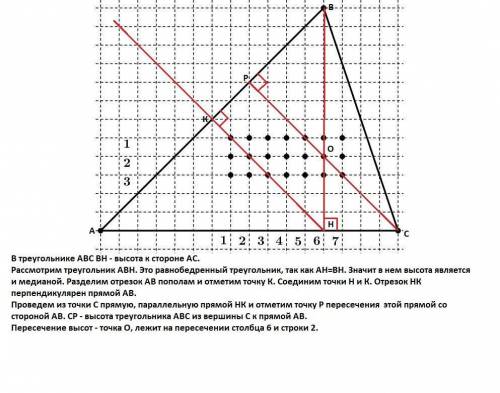
В треугольнике АВС ВН - высота к стороне АС.
Рассмотрим треугольник АВН. Это равнобедренный треугольник, так как АН=ВН. Значит в нем высота является и медианой. Разделим отрезок АВ пополам и отметим точку К. Соединим точки Н и К. Отрезок НК перпендикулярен прямой АВ.
Проведем из точки С прямую, параллельную прямой НК и отметим точку Р пересечения этой прямой со стороной АВ. СР - высота треугольника АВС из вершины С к прямой АВ.
Пересечение высот - точка О, лежит на пересечении
столбца 6 и строки 2.

160
Объяснение:
1) Со стороны тупого угла верхнего основания опускаем перпендикуляр на нижнее основание - трапеция разобьётся на две фигуры: прямоугольник и треугольник.
2) У прямоугольника противоположные стороны равны, поэтому нижняя сторона прямоугольника равна 16.
3) 24 - 16 = 8 - это основание треугольника.
Этот треугольник - равнобедренный, т.к. угол при основании равен 45°, согласно условию, а второй угол также равен 45°:
180 (сумма внутренних углов треугольника) - 45 - 90 = 45°.
Следовательно, вторая сторона треугольника (она же высота трапеции) равна 8.
4) Площадь трапеции равна произведению полусуммы её оснований на высоту:
((16+24) : 2) · 8 = 40 : 2 · 8 = 20 · 8 = 160
ответ: 160