ответ:Биссектриса равна
(24+24-36):2=12:2=6см
Два треугольника,которые образовались в результате проведения биссектрисы(треугольники АВМ и МВС) равны между собой по второму принципу равенства треугольников
ВМ-общая сторона
<АВМ=<МВС,т к биссектриса поделила угол В треугольника АВС на два равных угла
<АМВ=<ВМС,т к биссектриса в равнобедренном треугольнике,при условии,что она опущена из вершины на основание,является еще и высотой,т е перпендикуляром на основание и образовывает два угла по 90 градусов
Равенство треугольников доказано,следовательно периметр каждого равен 24 см
Распишем периметр треугольника АВС
Р=АВ+ВС+АМ+МС=36 см
Теперь-периметры треугольников АВМ и МВС
Р=АВ+ВС+АМ+МС+(ВМ+ВМ)=24+24=48
ВМ- биссектриса и она равна
(48-36):2=12:2=6 см
Объяснение:
Дано: А(-3; 9), В(-4; -8), С(6; 0)
Найти:
а)координаты вектора АС;
б)длину вектора ВС;
в)координаты середины отрезка АВ:
г)периметр треугольника АВС;
д)длину медианы СМ.
a) AC = {Cx - Ax ; Cy - Ay}
AC = {6 - (-3) ; 0 - 9}
AC ={9 ; -9}
б) BC = {Cx - Bx ; Cy - By}
BC = {6 - (-4); 0 - (-8)}
BC = {10 ; 8}
|BC| =  =
= 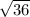 = 6
= 6
в) Пусть это будет точка M, тогда её координаты будут равны
M((Ax + Bx)/2 ; (Ay + By)/2)
M((-3 + -4)/2 ; (9 + 8)/2)
M(-3,5 ; 8,5)
г) Посчитаем длину каждой стороны треугольника
AB = 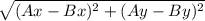 =
= 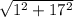 =
= 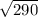
AC = 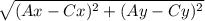 =
= 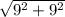 =
= 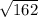
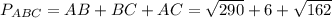
д) СМ = 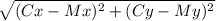 =
= 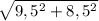 =
= 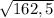
В равнобедренном треугольнике высота, проведённая к основанию, является также его медианой и биссектрисой.
Т.к КМ по условию является высотой и медианой,то треугольник АКВ -равнобедренный и АК=ВК.