
треугольник 2:
угол А = 180-100=80° - как смежные углы
угол С = внешнему углу С = 80° - как вертикальные углы
(угол В= 180-(80+80)=180-160=20 - как сумма всех кутов треугольника – ∆АВС не равносторонний)
свойство равнобедренных треугольников: куты у основания равны, значит ∆АВС равнобедренный
треугольник 3:
так как ВД=ВЕ,
ВА=ВС
за признаком равенства треугольников по двум сторонам и углу между ними: ∆АВС=∆ДВЕ
свойство равнобедренных треугольников: два катета равны (ВА=ВС)
значит ∆АВС равнобедренный
1см
Объяснение:
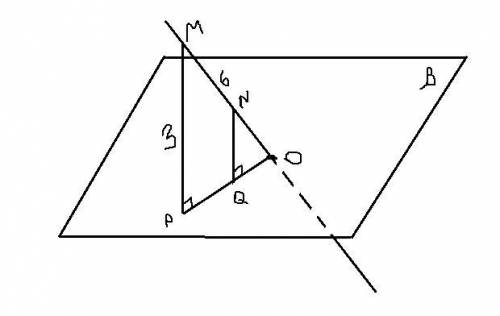
Точка N может лежать по одну сторону от плоскости β с точкой М или по другую. Если N лежит по другую сторону, то невозможно выполнить условия MN = 6 см и при этом OM = 9 см. Поэтому рассматриваем только случай, когда M и N находятся по одну сторону от плоскости β.
В этом случае расстояние от M до плоскости (определяется перпендикуляром, опущенным на эту плоскость) равно PM=3см. А расстояние от N до плоскости - QN.
Рассмотрим тр-ки MPO и NQO. Они подобны (2 угла прямые, а ещё один угол MOP общий). Значит PM/QN=OM/ON. ON=9-6=3
QN=PM*ON/OM=3*3/9=1
пусть m – точка пересечения диагоналей ac и bd четырёхугольника abcd. применим неравенство треугольника к треугольникам abc, adc, bad и bcd: ac < ab + bc, ac < da + dc, bd < ab + ad, bd < cb + cd. сложив эти четыре неравенства, получим: 2(ac + bd) < 2(ab + bc + cd + ad).
запишем неравенства треугольника для треугольников amb, bmc, cmd и amd: am + mb > ab, bm + mc > bc, mc + md > cd, ma + md > ad. сложив эти неравенства, получим: 2(ac + bd) > ab + bc + cd + ad.
внешний угол А равен 100*, соответственно внутренний угол А будет равен 80*. по свойству смежнего угла
угол С равен 80*; значит и внешний угол будет равен 80*. это по свойству вертикального угла.
угол А = угол С
вот и доказали равнобедренность треугольника