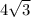 см
см
Объяснение:
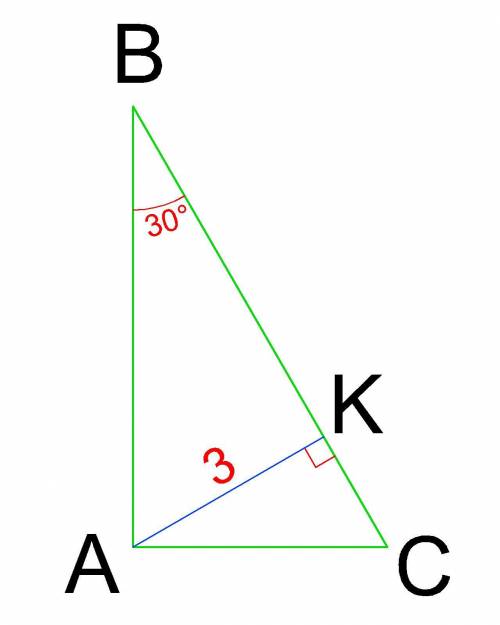
Побудуємо прямокутний ΔАВС, з висотою АК=3 см і гострим ∠В=30°.
І варіант рішення:
1) Розглянемо прямокутний ΔКВА.
Гіпотенуза АВ=АК/sin(B) ⇒ АВ=3/0,5=6 (см)
Катет ВК=АК/tg(B) ⇒ BK=3√3 (см)
2) Трикутники АВС, КВА та КАС подібні між собою (за гострим кутом як прямокутні трикутники). Тому
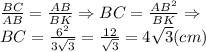
ІІ варіант рішення:
1) Розглянемо прямокутний ΔКВА.
Гіпотенуза АВ=АК/sin(B) ⇒ АВ=3/0,5=6 (см)
2) Розглянемо прямокутний ΔКАС.
В ньому ∠С=180°-90°-∠В=60°.
Гіпотенуза АС=АК/sin(С) ⇒ АС=3*2/√3=6/√3 (см)
3) Розглянемо ΔАВС.
Гіпотенуза 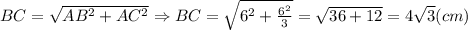
медиана в равнобедренном треугольнике является и высотой ,значит треугольник АВД-прямоугольный
следует ,что АВ=в= 18-а является гипотенузой АВД, АД=а -Ккатет АД
исходя из свойств гипотенузы и катета,получаем,что
2 2 2
(18- а) - а = 6
раскроем скобки
2 2
324- 36 а + а - а =36
квадраты а сокращаются
остается 324-36 а=36
отсюда убираем минусы так как с обоих сторон
остается 36 а= 324-36
36а= 288
а=288 : 36
а= 8 см
18- 8 =10 см= АВ=ВС
АС= 8+8=16 так как медиана делит пополам
периметр АВС=10+10+16=36 см