
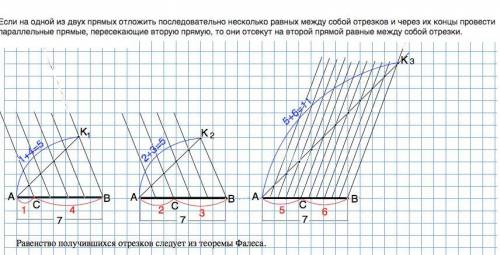
Объяснение (подробно):(см. рисунок приложения.)
Чертим отрезок АВ=7 см. Из А проведем луч и отложим на нем равные отрезки заданным числом. Конец последнего отрезка соединим с концом В заданного отрезка. Через концы отложенных на луче отрезков проведем прямые, параллельные прямой ВК. (Если не помните, как провести прямую, параллельную данной, найдите в учебнике, и в интернете на эту тему много информации).
а) на проведенном луче отложим 1+4=5 равных отрезков. Прямые, параллельные К1В, делят АВ на 5 равных частей. Часть АС=1, часть СВ=4. Длину получившихся отрезков можно посчитать на калькуляторе.
АС=7:5•1 (см); СВ=7:5•4(см)
б) отрезок АВ тем же делим на 2+3=5 частей.
АС=7:5•2 (см); СВ=7:5•3 (с м)
в) аналогично на проведенном луче отложим 5+6=11 равных частей, и отрезок АВ делится на 11 равных частей.
АС=7:11•5 (см); СВ=7:11•6 (см)
1)3
2)0°
Объяснение:1) 3sin (arccos0)=3sin (π/2)=3*1=3
2) 5arcsin (cos π/2)=5arcsin0=0
Напомню, что арксинусом числа а называют угол из отрезка [-π/2;π/2], синус которого равен а.
арккосинусом числа а называют угол из отрезка [0;π], косинус которого равен а.
Т.е. арккосинус нуля равен π/2, т.к. это угол из отрезка [0;π], косинус угла π/2 есть нуль.
арксинус нуля есть нуль. т.к. нуль входит в отрезок [0;π], и синус нуля равен нулю.
Косинус π/2 равен нулю . Во втором задании нуль градусов равен нулю радиан.