меньший катет АС=6см, больший катет ВС=12√3 см
Объяснение:
обозначим вершины треугольника А В С с прямым углом С катетами АС и ВС и гипотенузой АВ. Проекции катетов на гипотенузу образует высота СН проведённая из вершины прямого угла, поэтому СН перпендикулярно АВ. СН также делит ∆АВС на 2 прямоугольных треугольника АСН и СВН в которых АН, ВН, СН - катеты, а АС и ВС - гипотенузы. Он подобны между собой, так как высота проведённая из вершины прямого угла делит его на прямоугольные треугольники подобные между собой и каждый из них подобен ∆АВС. АВ=АН+ВН=6+18=24 см. Рассмотрим ∆АСН и ∆АВС. В ∆АСН АС является гипотенузой, а в ∆АВС - гипотенуза АВ, поэтому гипотенуза АС~ гипотенузе АВ. А также меньший катет ∆АСН АН~ АС(меньшему катету ∆АВС:
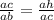
теперь подставим наши значения в эту пропорцию:
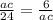
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
АС ²=6×24=144
АС=√144=12см
Теперь найдём катет ВС по теореме Пифагора:
ВС²=АВ²–АС²=24²–12²=576–144=432=12√3см

1) 1м.
2) 21 кв. ед.
3) 34.25 кв. ед.
Объяснение:
Дано. Стороны грядки, имеющей форму прямоугольника, равны 2,5 м и 0,4м.
Найти периметр грядки, равновеликой данной и имеющей форму квадрата.
Решение.
Равновеликие прямоугольник и квадрат у которых равные площади.
Найдем площадь прямоугольника
S=ab = 2.5 * 0.4 = 1 м².
S квадрата = S прямоугольника
S квадрата =a²; a²=1;
a=±1; (-1 - не соответствует условию.)
а=1 м.
Равновеликим прямоугольнику со сторонами 2,5 м и 0,4 м является квадрат со стороной 1 м.
***
2) Дано. ABCD - трапеция. AB=6; BC=4; AD=10; угол A=30*.
Найти площадь.
Решение.
Проведем высоту ВЕ. Получили треугольник АВЕ, в котором угол А=30* АВ=6 - гипотенуза. АЕ и ВЕ - катеты, а ВЕ=h - еще и высота трапеции.
BE =h = AB* sin 30*=6*1/2=3.
Площадь S=h(a+b)/2 = 3*(10+4)/2=3*14/2=21 кв. ед.
***
3) Дано. Δ ACD, у которого ∠А=30°; ∠ACB=60°; внешний угол D = 135°; BC=5 - высота. Найти площадь.
Решение.
В Δ BCD внутренний угол В = 180°-135° = 45°. Следовательно Δ BCD - равнобедренный ВС=BD = 5.
Из Δ АВС АВ = ВС/ tg30° = 5/0.577 = 8,7.
AD = 8,7 + 5=13,7.
Площадь S=1/2*AD*BC = 1/2* 13.7*5 = 34.25 кв. ед.