Сторони трикутника дорівнюють 5см і 7см утворюють кут градусна міра якого становить дві третіх градусних міри прямого кута. Чому дорівнює радіус кола описаного навколо трикутника

👇

Увидеть ответ

Ответ:

Катер007

08.01.2023

$R = \sqrt{13}$ см.

Объяснение:

Смотрите фотографию.

Сторони трикутника дорівнюють 5см і 7см утворюють кут градусна міра якого становить дві третіх граду

4,5(13 оценок)

Открыть все ответы

Ответ:

NoZeX1

08.01.2023

ответ:

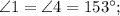
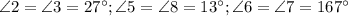№1: $\angle 7$ . №2: $\angle 1 = \angle 4 = 153^{\circ};$ $\angle 2 = \angle3 = 27^{\circ}; \angle 5 = \angle 8 = 13^{\circ}; \angle 6 = \angle 7 = 167^{\circ }$ .

Объяснение:

№1.

Пусть a || b , тогда - секущая.

Теорема: "При пересечении двух параллельных прямых секущей, сумма односторонних углов равна $180^{\circ}$ .

a || b , по условию.

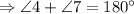
$\angle 4$ и $\angle 7$ - односторонние углы $\Rightarrow \angle 4 + \angle 7 = 180^{\circ}$

№2.

Обозначим данные прямые буквами 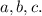a, b, c.

Пусть - секущая прямых и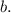

Теорема: "При пересечении двух параллельных прямых секущей, накрест лежащие углы равны".

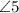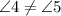$\angle 4$ и $\angle 5$ - накрест лежащие при пересечении и секущей , однако $\angle 4 \neq \angle 5$ .

$\Rightarrow$ и - не параллельны.

============================================================

Свойство: "Вертикальные углы равны".

Свойство: "Сумма смежных углов равна $180^{\circ}$ ".

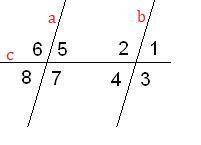
Рассмотрим углы, образовавшиеся при пересечении прямых и

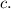
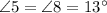$\angle 5 = \angle 8 = 13^{\circ}$ , по свойству вертикальных углов.

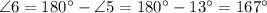$\angle 6 = 180^{\circ} - \angle 5 = 180^{\circ} - 13^{\circ} = 167^{\circ}$ , по свойству смежных углов.

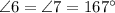$\angle 6 = \angle 7 = 167^{\circ}$ , по свойству вертикальных углов.

===========================================================

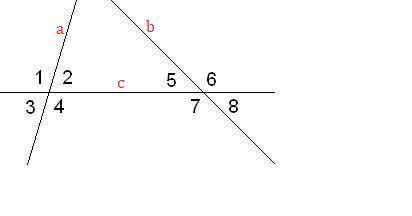
Рассмотрим углы, образовавшиеся при пересечении прямых и .

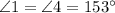$\angle 1 = \angle 4 = 153^{\circ}$ , по свойству вертикальных углов.

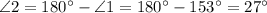$\angle 2 = 180^{\circ} - \angle 1 = 180^{\circ} - 153^{\circ} = 27^{\circ}$ , по свойству смежных углов.

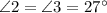$\angle 2 = \angle 3 = 27^{\circ}$ , по свойству вертикальных углов.

1.две параллельные прямые пересекаются с третьей прямой. найди углы, сумма которых с данным углом р

4,6(95 оценок)

Ответ:

Havedid

08.01.2023

В равнобедренной трапеции диагональ является биссектрисой острого угла . Основание трапеции относится к боковой стороне как 8:5 Периметр трапеции равен 69 см найти стороны трапеции.

Объяснение:

АВСД-трапеция, АВ=СД , АД:АВ=8:5 , Р=69 см.

Тк. ВС║АД , АС-секущая , то ∠САД=∠АСД как накрест лежащие .

Тогда ΔАВС-равнобедренный по признаку ⇒АВ=ВС= 5 частей.

Поэтому СД=5 частей. Т.к. АД:АВ=8:5 , то АД= $\frac{8}{5}$ *АВ.