На основании утверждения о катете прямоугольного треугольника:
АС = корень AB*AD , СВ = корень AB*DB.
Возведем в квадрат и сложим полученные равенства:
АС² = АВ * АD, СВ² = АВ * DВ;
АС² + СВ² = АВ * ( АD + DВ), где АD+DB=AB, тогда
АС² + СВ² = АВ * АВ,
АС² + СВ² = АВ².
ответ: 12 (ед. площади)
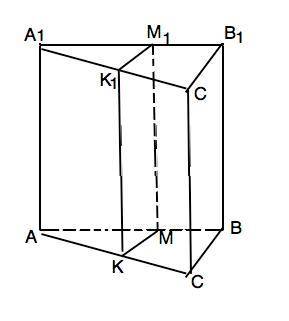
Объяснение: Площадь боковой поверхности призмы равна произведению высоты призмы на периметр основания: S=Н•Р=24
При проведении плоскости через среднюю линию основания параллельно боковому ребру плоскость сечения отсекает от оснований равные треугольники, подобные треугольникам оснований с коэффициентом подобия k=0,5а:а=1/2. Периметры подобных фигур относятся как их линейные размеры. Следовательно, S₂(бок)=Н•Р/2. Т.к. высота призмы не изменилась, S₂(бок)=24•1/2=12 (ед. площади)
Доказательство теоремы Пифагора
Пусть треугольник ABC - прямоугольный треугольник с прямым углом C
Проведём высоту из вершины C на гипотенузу AB, основание высоты обозначим как H .
Прямоугольный треугольник ACH подобен треугольнику ABC по двум углам ( ∠ACB=∠CHA=90∘∠ACB=∠CHA=90∘, ∠A∠A - общий). Аналогично, треугольник CBH подобен ABC .
Введя обозначения
BC=a,AC=b,AB=cBC=a,AC=b,AB=c
из подобия треугольников получаем, что
ac=HBa,bc=AHbac=HBa,bc=AHb
Отсюда имеем, что
a2=c⋅HB,b2=c⋅AHa2=c⋅HB,b2=c⋅AH
Сложив полученные равенства, получаем
a2+b2=c⋅HB+c⋅AHa2+b2=c⋅HB+c⋅AH
a2+b2=c⋅(HB+AH)