Трапеция АВСД, АВ=СД, уголА=уголД, ВС=37, АД=61, АС-биссектриса углаА = диагональ
угол САД=уголАСВ как внутренние разносторонние=уголСАВ, треугольник АВС равнобедренный, ВС=АВ=СД=37, проводим высоты ВН и СК на АД, треугольники АВН=треугольник КСД по гипотенузе АВ=СД и острому углу уголА=уголД, КД=АН, четырехугольник НВСК прямоугольник ВС=НК=37, АН=КД=(АД-НК)/2=(61-37)/2=12
треугольник АВН, ВН=корень (АВ в квадрате-АН в квадрате) = корень(1369-144)=35
Площадь = (ВС+АД)/2 х ВН =(37+61)/2 х 35=1715
Объяснение:
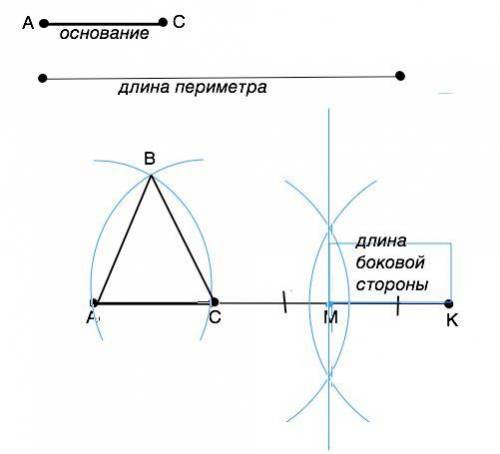
1) На произвольной прямой отложить отрезок, равный длине периметра. Обозначить его АК.
2) От т.А циркулем отметить на АК точку С, АС= длине данного основания.
3). Отрезок СК разделить на две равные части. Для этого из т.С и т.В провести две полуокружности до их пересечения по обе стороны от СК. Точки пересечения соединить прямой ( срединным перпендикуляром). Точку пересечения этой прямой и отрезка СК обозначить М. СМ=МК=длина боковой стороны треугольника.
4). Циркулем с раствором, равным МК, провести из точек А и С дуги до их пересечения. Точку пересечения обозначить В и соединить с т.А и т.С. Треугольник АВС - искомый.
a3 = 2rsqrt3
a3 = 2*2/3*sqrt3
a3 = 4sqrt3/3
a3 = Rsqrt3
R = a3/sqrt3
R = 4/3 = 1 целая 1/3
ОТвет 4/3