если нижнее основание а, верхнее b, и искомый отрезок - длины х, то прощади трапеций будут такие
S1 = (b + x)*h1/2; S2 = (a + x)*h2/2;
или, поскольку S1 = S2,
(b + x)/(a + x) = h2/h1;
Чтобы получить соотношение между h1 и h2, проведем прямую, параллельную боковой стороне через конец отрезка х, лежащий на ДРУГОЙ боковой стороне.
Малое основание продолжим до пересечения с этой прямой. Получилось 2 подобных треугольника с основаниями (x - b) и (a - x); из подобия следует
h2/h1 = (a - x)/(x - b);
поскольку соответствующие высоты так же пропорциональны, как и стороны.
Итак, имеем уравнение для х
(b + x)/(a + x) = (a - x)/(x - b);
x^2 - b^2 = a^2 - b^2;
x = корень((a^2 + b^2)/2);
Подставляем численные значения, получаем
х = корень(24^2 + 7^2) = 25;
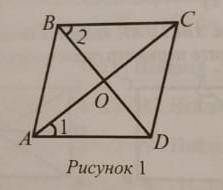
2) Площадь ромба равна половине произведения диагоналей:
3) От какой точки?.. Точка как расположена? На окружности?
До концов каких диаметров? Или до концов одного диаметра?
Если моё хорошее знание геометрии позволило мне правильно догадаться до сути задания, то имеется ввиду точка на окружности, и расстояние от неё до концов диаметрА равно 12 и 16.
Тогда видим вписанный угол, опирающийся на диаметр, равный 90⁰, ну и, соответственно, прямоугольный треугольник, с катетами 12 и 16 и гипотенузой, равной диаметру окружности.
Как "Лучшее решение" не забудь отметить, ОК?!.. ;)))