Расстоянием от точки до прямой называет длина перпендикуляра, проведённого из этой точки на прямую. Поэтому надо найти длину перпендикуляра. Пусть длина перпендикуляра равна x, тогда длина наклонной равна y. Составим систему уравнений, учитывая, что x + y = 17, а y - x = 1
x + y = 17 2y = 18 y = 9
y - x = 1 y - x = 1 x = 8
Длина перпендикуляра равна 8, поэтому и искомое расстояние тоже равно 8.
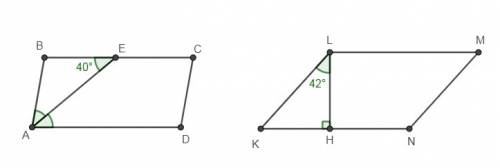
а) Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник ⇒ ∠ВАЕ = ∠ВЕА = 40°
∠А = 2∠ВАЕ = 2 * 40 = 80° (так как АЕ - биссектриса ∠А)
Сумма соседних углов параллелограмма равна 180° ⇒
∠В = 180 - ∠А = 180 - 80 = 100°
Противоположные углы параллелограмма равны ⇒
∠С = ∠А = 80°
∠D = ∠В = 100°
ответ: 80°; 80°; 100°; 100°.
-------------------------------------------------------------------------
б) ΔKLH - прямоугольный ⇒ ∠К = 90 - 42 = 48°
Сумма соседних углов параллелограмма равна 180° ⇒
∠L = 180 - ∠K = 180 - 48 = 132°
Противоположные углы параллелограмма равны ⇒
∠M = ∠K = 48°
∠N = ∠L = 132°
ответ: 48°; 48°; 132°; 132°.
Проведи окружности с заданным радиусом через каждую точку. Две точки пересечения и будут центрами искомой окружности (т.е. их две) или если расстояние между ними равно 2 радиусам, окружность будет одна