∠XIaY=114°
Объяснение:
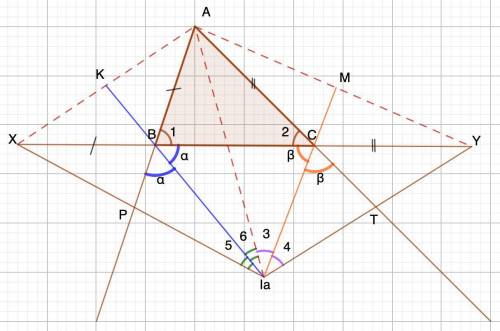
Дано: ΔАВС.
BIa - биссектриса ∠РВС; СIa - биссектриса ∠ВСТ;
ХВ=АВ; АС=СY;
∠ВАС=66°.
Найти: ∠XIaY
1. ∠1+∠2=180°-66°=114° (сумма углов Δ)
∠1+2α=180° (развернутый)
∠2+2β=180° (развернутый)
∠1+∠2+2α+2β=360°
2(α+β)=360°-114°=246° ⇒ α+β=123°
2. Рассмотрим ΔBCIa.
∠BIaC=180°-(α+β)=180°-123°=57° =∠6+∠3 (сумма углов Δ)
3. Рассмотрим ΔХВА - равнобедренный.
∠XBA=∠KBA=α ⇒ ВК - биссектриса, медиана, высота (свойство р/б Δ)
4. Рассмотрим ΔACY - равнобедренный.
∠АСМ=∠MCY=β ⇒ CM - биссектриса, медиана, высота (свойство р/б Δ)
5. Рассмотрим ΔXIaA.
IaK - высота, медиана (п.3) ⇒ ΔXIaA - равнобедренный
⇒ IaK - биссектриса ⇒ ∠5=∠6.
6. Рассмотрим ΔAIaY.
IaM - высота, медиана ⇒ ΔAIaY - равнобедренный
⇒ IaM - биссектриса ⇒ ∠3=∠4
7. ∠XIaY=∠5+∠6+∠3+∠4=2*(∠6+∠3)=2*57°=114°
Объяснение:
1)Точки F и E-середины сторон BC и BA треугольника ABC.
Отрезок, соединяющий середины двух сторон треугольника, является его средней линией, равен половине третьей стороны и параллелен ей.
АЕ=ВЕ=10 => АВ=10•2=20 см
CF=BF=> ВС=16•2=32 см
АС=EF•2=14•2=28 см.
Периметр треугольника - сумма длин его сторон.
Р(АВС)=20+28+32=80 см
Вариант решения.
Так как отрезок ЕF – средняя линия ∆ АВС и параллелен АС, углы при основаниях ∆ АВС и ∆ ВЕF равны как соответственные углы при пересечении параллельных прямых секущими АВ и СВ, и угол В - общий.
Поэтому ∆ АВС~∆ ВЕF по равным углам.
АВ=2•ВЕ=>
Коэффициент подобия этих треугольников равен АВ:ВЕ. k=2
Р(BEF)=BE+BF+EF=40 см
Отношение периметров подобных фигур равно коэффициенту подобия их линейных размеров. ⇒
Р(АВС)=2Р(BEF)=2•40=80 см
2) Примем меньшее основание трапеции равным а. Тогда большее – 2а
Средняя линия трапеции равна половине суммы оснований.
6=( а+2а):2
а+2а=12
3а=12 ⇒ а=12:3=4
Меньшее основание трапеции равно 4 см.
Большее 4•2=8 см
Если прямая и плоскость имеют две общие точки, то вся прямая принадлежит этой плоскости.