Диагональ AC = 8см
Объяснение:
Если угол BAD = 120, то угол BAC = 60 (т.к. AC это диагональ ромба, а диагонали ромба делят его углы пополам).
Угол BAC = углу BCA = 60 (т.к. AC это диагональ ромба)
А если два угла треугольника равняются 60 градусам, то и третий равен 60, поэтому угол ABC = 60.
А если все углы треугольника равны, то и стороны тогда равны и треугольник равносторонний.
В таком случае имеем:
AB = BC = AC
Если AB + BC + CD + DA = 24см, а все стороны ромба равны, то
AB = BC = CD = DA =  = 8см, то
= 8см, то
AB = AC = 8см
Больший угол ромба равен 120°.
Объяснение:
Диагонали ромба равны а и а√3. Найдите больший угол ромба.
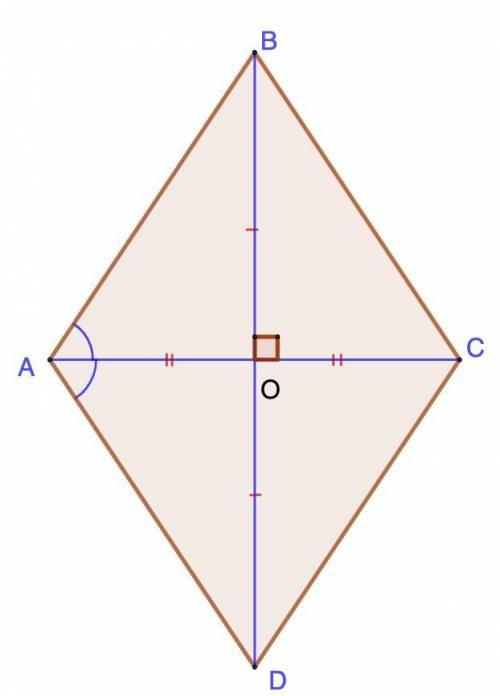
Дано: ABCD - ромб;
АС и BD - диагонали;
AC = a; BD = a√3.
Найти: ∠А.
Рассмотрим ΔАВО.
Диагонали ромба взаимно перпендикулярны.⇒ ΔАВО - прямоугольный.
Диагонали ромба точкой пересечения делятся пополам.⇒
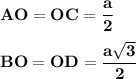
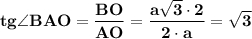
⇒ ∠BAO = arctg (√3) = 60°
Диагонали ромба являются биссектрисами его углов.⇒ ∠ВАО = ∠OAD = 60°
Тогда ∠А = ∠ВАО + ∠OAD = 120°
Больший угол ромба равен 120°.
4
Объяснение:
АД=Cos30°*4tg60