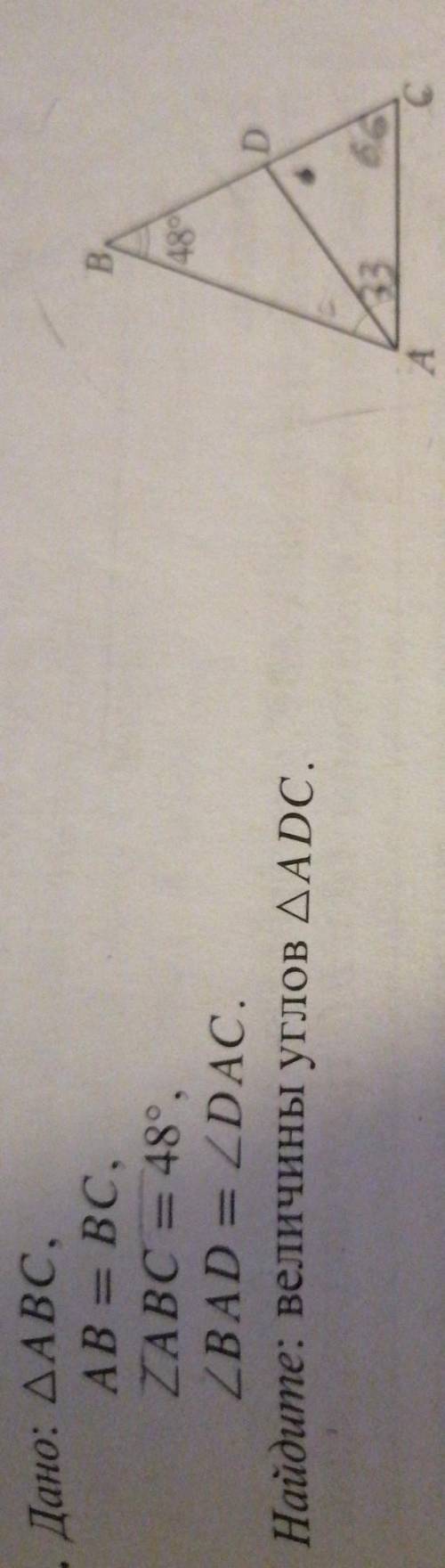
<ADC=81°
<DCA=66°
<DAC=33°Объяснение:
Объяснение:
1.Угол, вершина которого лежит в центре окружности называется
А) центральным;
2. Угол, вершина которого лежит на окружности называется
Б) вписанным;
3. Вписанный угол равен
В) половине дуги на которую он опирается.
4. Центральный угол равен
Б) дуге, на которую он опирается;
5. Чему равен вписанный угол, опирающийся на дугу в 120°
Б) 60°;
6. Чему равен центральный угол, опирающийся на дугу в 40°
В) 40°
7. Чему равен вписанный угол, опирающийся на дугу в 100°
А) 50°;
8.Чему равен центральный угол, опирающийся на дугу в 80°
Б) 80°;
Запишите ответ (задания 9-12):
9. Найдите <DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.
<DEF опирaтeся на дугу = 360°-(DE + EF)=360°-( 150° + 68° ) =142°.
<DEF - вписанный угол,
<DEF=1/2×142°=71°
10. Найдите <KOM, если известно, что градусная мера дуги MN равна 124°, а градусная мера дуги KN равна 180°. Точка O — центр окружности.
υMK=υKN-υMN=180°-124°=56°
<KOM - центральный угол,<KOM=56°
11. Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 48°.
<C - вписанный угол,= половине центральнoго углa AOB.
<C=1/2<AOB=1/2*48°=24°
12. Точка О — центр окружности, <AOB = 84° (см. рисунок). Найдите величину угла ACB (в градусах). Дай рисунок.
<ADC=81°
<DCA=66°
<DAC=33°
Объяснение:
Сумма углов в треугольнике равна 180°;
В равнобедренном треугольнике углы при основании равны.
∆АВС- равнобедренный по условию.
<ВАС=<ВСА.
<ВАС=(180°-<АВС)/2=(180°-48°)/2=138/2=66°
<ВСА=66°.
<BAD=<DAC, по условию (АD- биссектрисса).
<DAC=<BAC:2=66°:2=33°
Сумма углов в треугольнике равна 180°
∆DAC.
<DCA=66°;
<DAC=33°;
<ADC=180°-<DCA-<DAC=180°-33°-66°=81°