Объяснение:
АВСД -прямоугольная трапеция ,ВС=4√2 , ∠А=45°, ∠Д=90°, АС-биссектриса ∠А.
1)Т.к АС-биссектриса, то ∠САД=∠САВ.
2)Т.к. АД║ВС ( основания трапеции), АС-секущая, то ∠ДАС=∠ВСА , как накрест лежащие. Значит в ΔАСВ есть два равных угла по 22,5° ⇒ ΔАСВ-равнобедренный и ВС=ВА=4√2.
3)Пусть ВК⊥АД, тогда ΔВКА-прямоугольный и равнобедренный , т.к. ∠КВА=90°-45°=45°. Обозначим равные катеты через х. По т. Пифагора :х²+х²=(4√2)², 2х²=16*2, х=4, КА=ВК=4.
3)Т.к. ВК⊥АД, то ДК=4√2.
4)ΔДВК-прямоугольный, по т. Пифагора ДВ²=КВ²+КД²,
ДВ²=16+16*2,
ДВ²=3*16
ДВ=4√3
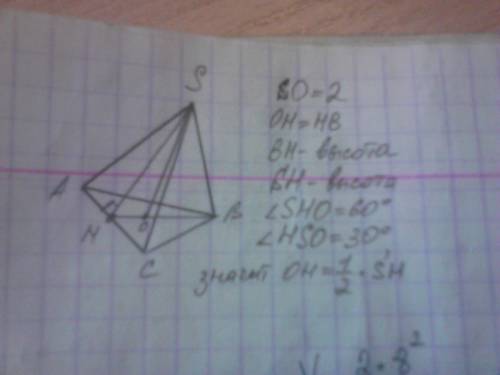
пусть SH(гипотенуза)- х см, тогда катет ОН=1/2SH(лежит напротив угла 30), тогда
по т пиФ высота SO^2=х^2-x^2/4=3x^2/4, тогда
т.к. SO^2=4, то справедливо 3x^2/4=4, поэтому х=4/корень из 3 см, тогда
ОН=1/2*SН=4/ 2 корня из 3 см=2 / корень из 3 см, тогда
т.к. основание - равносторонний треугольник, то ОН=ОВ, тогда
ВН=2*2 / корень из 3=4/корень из 3 см, тогда
найдем ВС, пусть ВС - у см, тогда
по т Пиф у^2-y^2/4=3y^2/4=16/3, тогда отсюда у^2/4=16, y^2=64, y=8 см,
значит объём найдем по формуле V=(SO*BC^2) / 4 корня из 3, подставим,
получим : V = (2*64)/4 корня из 3= 32 / корень из 3
ответ: объем пирамиды равен 32 / корень из 3 см кубических.
Удачи ! )
S = (6 + 10) / 2 * 8 = 64