Question

РЕШИТЬ ДВЕ ЗАДАЧИ!) условие и рисунок во вложении. БУДУ ОЧЕНЬ БЛАГОДАРЕН! И еще известно что площадь треугольника KLM равна а(3+2кор13)/6
если нужно будет

Answer 1

B1.   S = (a²√43)/48 ≈ 0.137 a²;    B2.    AE = 2a;

Объяснение:

У тетраэдра АВСD все рёбра равны а, следовательно, все углы между рёбрами граней равны по 60°.

По условию АК = КD, поэтому АК = КD = а/2.

По условию CL : LD = 1 : 2, следовательно CL = a/3, a  LD = 2a/3.

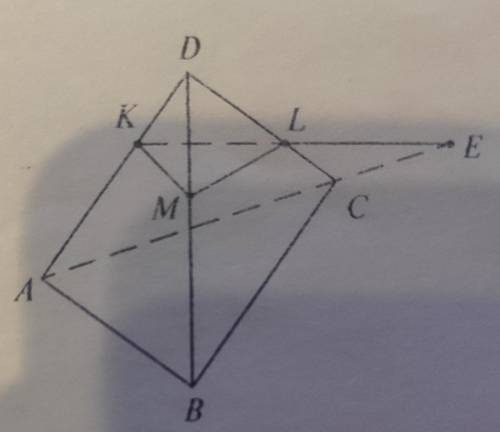
Смотри прикреплённый рисунок. Там сделаны дополнительные построения.

В1.

Из точки К проводим прямую KM, параллельную АВ и соединяем отрезком прямой точки М и L

Поскольку плоскость KLM параллельна АВ, то по определению параллельности прямой и плоскости (Если прямая, не лежащая в плоскости, параллельна прямой, лежащей в этой плоскости, то она параллельна данной плоскости) строим плоскость KLM следующим образом.

Проводим прямую КМ параллельно АВ и соединяем отрезком прямой точки М и L. По приведённому признаку параллельности прямая АВ параллельна плоскости KLM.

Поскольку КМ ║ АВ, то MD = BM = a/2

КМ - является средней линией ΔADB ⇒ КМ = а/2.

Рассмотрим Δ MDL. Найдём в нём сторону ML.

По теореме косинусов ML² = MD² + LD² - 2 · MD · LD · cos 60°

ML² = (a/2)² + (2a/3)² - 2 · a/2 · 2a/3 · 1/2

ML² = a²/4 + 4a²/9 - a²/3

ML² = 13a²/36

ML = (a√13)/6

ΔKDL = ΔMDL (KD = MD;  DL - общая сторона; и ∠KDL = ∠MDL = 60°)

Следовательно, KL = ML =  (a√13)/6

и ΔKML - равнобедренный  KL = ML =  (a√13)/6

Высота h в ΔKML является и медианой и делит пополам сторону КМ, которая равна а/2

Найдём h по теореме Пифагора

ML² = h² + (KM/2)²

13a²/36 = h² + (a/4)²

h² = 13a²/36 - a²/16 = 52a²/144 - 9a²/144 = 43a²/144

h = (а√43)/12

Площадь ΔKML равна

S = 1/2 · KM · h = 1/2 · a/2 ·  (а√43)/12

S = (a²√43)/48

В2.

В треугольнике АКЕ проведём прямую KF ║ СL.

Тогда ΔАКF - равнобедренный (так как ∠КFA = ∠KAF = 60°), и KF = AF = a/2;    и  FC = AC - AF = a - a/2 = a/2

ΔKFE и ΔLCE подобны, так как KF ║ LC.

Из их подобия следует, что

КF : LC = EF : EC

a/2 : a/3 = (FC + EC) : EC

3/2 = (a/2 + EC) : EC

3 EC/2 = a/2 + EC

EC/2 = a/2

EC = a

AE = AC + EC = a + a = 2a