
4 см
Объяснение:
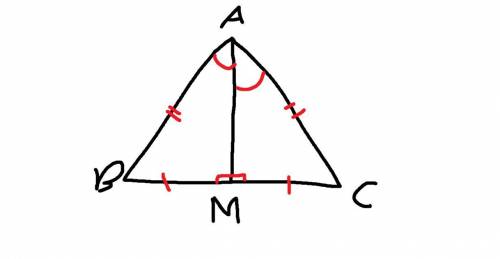
Так как высота АМ , проведённая из вершины равнобедренного треугольника, является медианой и биссектрисой, то углы ∠ВАМ и ∠САМ равны, а так как ∠ ВАС = 90 °, то они равны 45°.
Известно, что сумма углов треугольника равна 180°, значит в ΔСАМ ∠АСМ = 180° - 90° - 45° = 45°, а следовательно ΔСАМ - равнобедренный, что означает равенство сторон АМ и СМ
Высота АМ (медиана и биссектриса) делит сторону ВС на 2 равные части, а так как ВС = 8, то значит, что МС = 1/2 * 8 = 4, а так как МС = АМ, то и АМ = 4
ответ: 2) 2
7) 20°
Объяснение:
4) Средняя линия треугольника равна половине той его стороны, которая ей параллельна. На рисунке видно, что АВ занимает 4 клеточки, значит средняя линия будет 4/2=2 клеточки
7) Обозначим ∠А=2х, ∠В=7х. ∠С=8х
∠А+∠В=180° (как углы прилягающие к одной боковой стороне трапеции)
2х+7х=180°
9х=180° |:9
х=20°
∠C=8*20°=160°
По тому же свойству ∠C+∠D=180°
∠D=180°-∠C
∠D=180°-160°=20°