ответ:S=12P⋅h,S=12⋅9⋅7√2=97√4
Объяснение:
найдем сторону основания правильной пирамиды по формуле a = R√3, a = √ · √ = 3
найдем периметр основания Р = 3·а, Р = 9
радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. R = 2r, тогда OP=3√2
из прямоугольного треугольника МОР по теореме Пифагора находим апофему МР: MP=MO2+OP2−−−−−−−−−−√,
МР=1+|3√2|2−−−−−−−−√=1+34−−−−−√=7√2
вычислим площадь боковой поверхности правильной пирамиды: S=12P⋅h,S=12⋅9⋅7√2=97√4
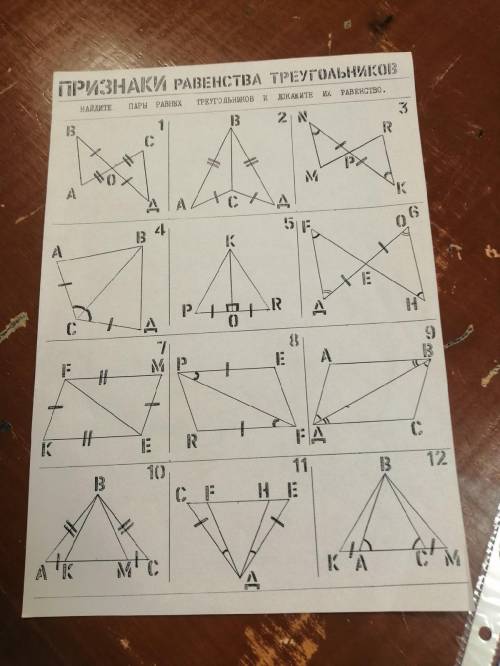
1. За двумя сторонами и углом между ними. BO=AO, CO=AO, BOA=COA
2. За тремя сторонами. BС -- общая, AB=BD, AC=AD
3. За стороной и прилежащими углами. NP=PK, RKP=PNM, NPM=RPK
4. За двумя сторонами и углом между ними. BC -- общая, AC=CD, ACB=DCB
5. За двумя сторонами и углом между ними. KO -- общая, PO=OR, POK=ROK (так как оба углы равны 90, что видно по квадратной пометке)
6. За стороной и прилежащими углами. AO=EO, DEF=EOH, FED=OEH
7. За тремя сторонами. FE -- общая, FM=KE, KF=ME
8. За двумя сторонами и углом между ними. FPE=RFP , PE=RF , PF -- общая
9. За двумя сторонами и углом между ними. BD -- общая, ABD=CDB, ADB=CBD
10. За двумя сторонами и углом между ними. AK=MC. BC=AB, так что треугольник ABC -- равнобедренный, отсюда BAK=BCM
Объяснение: