Допустим, что мы вписали параллелограмм в окружность, тогда попробуем провести 2 диагонали окружности так, чтобы они совпали с диагоналями параллелограмма и были,естественно, равны! Но это невозможно, т.к. в параллелограмме диагонали могут быть равными если только это прямоугольник(то 3 признак прямоугольника)! Тоесть параллелограмм, вписанный в окружность является прямоугольником! Что и требовалось доказать!
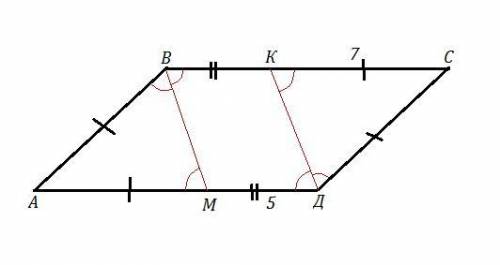
АВСД - параллелограмм , ВМ и ДК - биссектрисы , то есть ∠АВМ=∠МВС , ∠АДК=∠СДК , МД=5 см , КС=7 см .
Так как в параллелограмме противоположные углы равны, то ∠В=∠Д ⇒ ∠АВМ=∠СВМ=∠АДК=∠СДК .
Но ∠АМВ и ∠АДК - соответственные равные углы ⇒ ВМ ║ДК.
Так как АВСД - параллелограмм, то ВК ║ ДМ ⇒ МВКД - тоже параллелограмм, а значит ВК=ДМ=5 см.
∠АДМ=∠ДКС как внутренние накрест лежащие при параллельных АД и ВС и секущей КД . Но ∠АДМ=∠СДК (КД - биссектриса) ⇒ ∠СДК=∠КДС , а это углы при основании ΔДСК ⇒ ΔДСК - равнобедренный ⇒ КС=СД=7 см .
Периметр параллелограмма:
Р=2*СД+2*ВС=2*7+2*(ВК+КС)=14+2*(5+7)=14+2*12=14+24=38 см .
DC и АВ-основания трапеции ABCD, точка Е-середина стороны ВС. На средней линии трапеции выбрана точка F так, что CDFE-параллелограмм . Известно , что S(ABCD)=38 см² и S(CDFE)=10 см² . Найдите площадь четырехугольника DAEF.
Объяснение:
S(DAEF)=S(DAE)-S(DFE), чертеж 1 . Продолжим часть средней линии трапеции → МЕ.
1) Чертеж 2 ; S(DAE)=S(DЕМ) +S(АЕМ)=
= (опустим высоты Δ DEM, ΔAEM)=
=1/2*МЕ*DP+1/2*ME*AH=1/2*ME*(DP+AH)=( сумма высот
треугольников будет равна высоте трапеции)=1/2*ME*h=
=1/2 *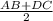 
*h=1/2*S(ABCD)=1/2*38=19(cм²).
2)S(DFE)=( диагональ параллелограмма делит его на два
равновеликих треугольника) = 1/2*S(СDFE)=1/2*10=5 (см²).
S(DAEF)=S(DAE)-S(DFE)=19-5=14 (см²) .
впишем произвольный параллелограм в окружность. с центра окружности проведем радиусы к вершинам фигуры. это невозможно. т.к в паралеллограмме диагонали должны быть равными, а это возможно в прямоугольнике