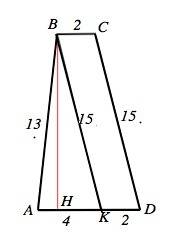
Обозначим трапецию АВСD.
АВ=13 см, СD=15 см, ВС=2 см, AD=6 см. ВН - высота трапеции.
Через вершину В проведем ВК параллельно СD.
Противоположные стороны четырехугольника КВСD параллельны – КВСD - параллелограмм, KD=ВС=2 см
Тогда АК=4 см.
Площадь ∆ АВК по ф. Герона , где р - полупериметр,
равна √(p•(p-AB)•(p-BK)•(p-AK)=√16•3•1•12)=24 см²
ВН =высота трапеции=высота ∆ АВК.
Из формулы площади треугольника
h=2S:a, где а- сторона, к которой высота проведена.
ВН=48:4=12 (см)
Площадь трапеции равна произведению высоты на полусумму оснований.
S(ABCD)=12•(2+6):2=48 см*
1) △АВС-р/б (по св-ву р/б △(углы при основание равны)
2)∠BOA=90°(по св-ву р/б △).
Буду очень признателена если поставишь корону и лайкушку!