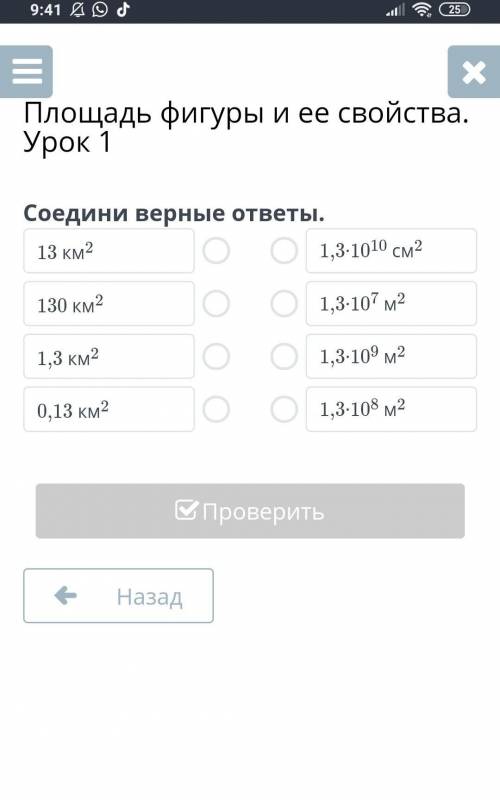
Площадь фигуры и ее свойства. Урок 1 Соедини верные ответы
13 км2
130 км2
1,3 км2
0,13 км2
1,3∙1010 cм2
1,3∙107 м2
1,3∙109 м2
1,3∙108 м2

Question

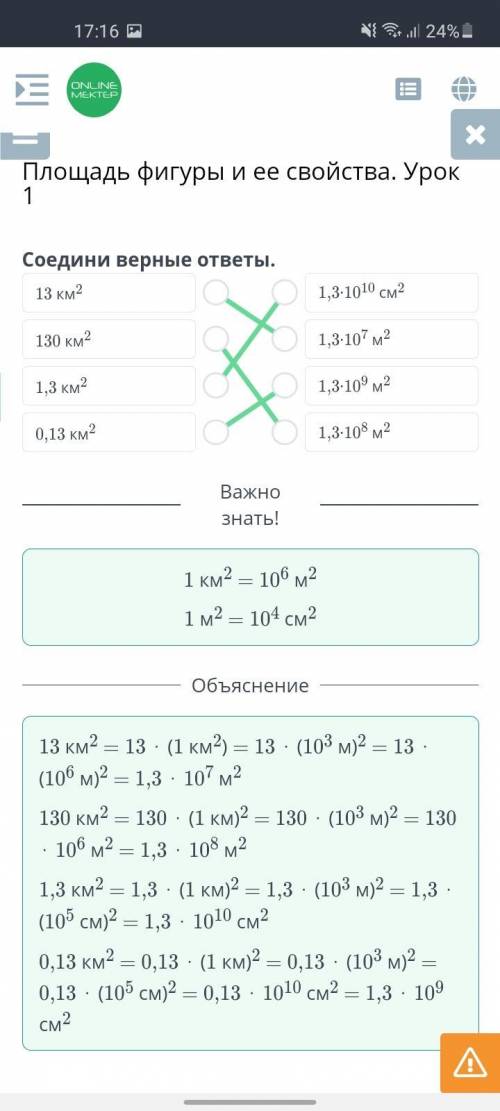
Геометрия: Площадь фигуры и ее свойства. Урок 1 Соедини верные ответы 13 км2 130 км2 1,3 км2 0,13 км2 1,3∙1010 cм2 1,3∙107 м2 1,3∙109 м2 1,3∙108 м2​

Meowcots · Accepted Answer

Равновеликие фигуры — это такие фигуры, площади которых между собой равны.

Докажем, что S(ABCD) = S(EBCF).

Доказательство :

Так как по условию ABCD — прямоугольник, то AB⊥ED.

Рассмотрим параллелограмм EBCF.

Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.

Следовательно, S(EBCF) = АВ×EF.

EF = BC (по свойству параллелограмма).

Тогда также верно равенство S(EBCF) = АВ×ВС.

Рассмотрим прямоугольник ABCD.

Площадь прямоугольника равна произведению его смежных сторон.

Следовательно, S(ABCD) = AB×BC.

Итак, так как правые части выражений равны, то мы можем приравнять из левые части. То есть мы получаем, что S(ABCD) = S(EBCF).

Что требовалось доказать.

Площадь фигуры и ее свойства. Урок 1 Соедини верные ответы13 км2130 км21,3 км20,13 км21,3∙1010 cм21,3∙107 м21,3∙109 м21,3∙108 м2​