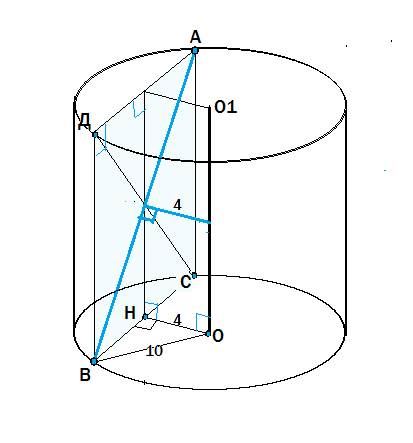
В равностороннем треугольнике все углы равны 60°.
Высоты, по свойству высоты равнобедренного треугольника, являются биссектрисами и медианами, и каждая делит его на 2 равных прямоугольных треугольника.
Высота в таких треугольниках является большим катетом, который противолежит углу 60°, сторона равностороннего треугольника- гипотенузой, а меньший катет противолежит углу 30° и равен половине гипотенузы (свойство)
-----------------
Примем меньший катет (половину стороны) равным а. Тогда гипотенуза (сторона равностороннего треугольника) равна 2а.
По т.Пифагора с²=a²+b² (с- гипотенуза, а и b- катеты)⇒
(2а)²=а²+((13√3)²⇒
3а²=13²•3 ⇒ а=13,
Сторона данного равностороннего треугольника 2а=26 (ед. длины)
или
с=b:sin60°, где с - сторона равностороннего треугольника, b- его высота.
с=(13√3):(√3/2)=26 (ед. длины)
Дано :
Цилиндр.
Прямоугольник ABCD — осевое сечение цилиндра.
ОН — высота цилиндра.
OD = 6 см, OH = 5 см.
Найти :
АС = ?
Образующая и высота цилиндра равны.Поэтому ОН = CD 5 см.
AD — это диаметр основания цилиндра, поэтому он будет в 2 раза больше радиуса OD. То есть AD = 2×OD = 2×6 см = 12 см.
Рассмотрим ∆ACD — прямоугольный (∠D = 90°).
По теореме Пифагора : AC² = AD² + CD² = 12² + 5² = 144 + 25 = 169⇒AC = √169 = 13 см.
13 см.