Дано: треугольник ABC - равнобедренный;
BD - биссектриса;
угол ABD = 34°;
AC = 24 см
Найти: угол B; угол BDC; сторону DC
1) ∠В = 2 × ∠ABD = 2 × 34° = 68°, т. к. BD - биссектриса делит Abc на равные углы.
2) треугольник ABC - равнобедренный => биссектриса, проведённая к основанию, является высотой => BD⊥AC и ∠BDC = 90°.
3) треугольник ABC - равнобедренный => биссектриса, проведённая к основанию, является медианой => DC = 1/2 × AC = 1/2 × 25 = 12,5 см.
ответ: ∠В = 68°; ∠BDC = 90°; DC = 12,5 см.
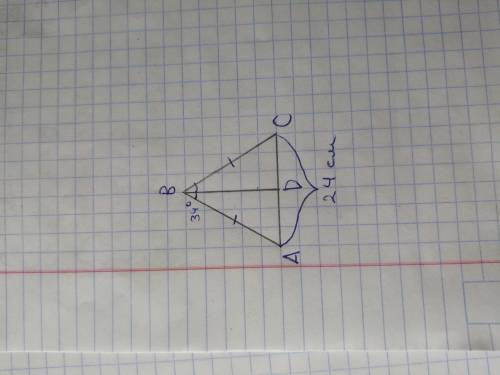
Дано: треугольник ABC - равнобедренный;
BD - биссектриса;
угол ABD = 34°;
AC = 24 см
Найти: угол B; угол BDC; сторону DC
1) ∠В = 2 × ∠ABD = 2 × 34° = 68°, т. к. BD - биссектриса делит Abc на равные углы.
2) треугольник ABC - равнобедренный => биссектриса, проведённая к основанию, является высотой => BD⊥AC и ∠BDC = 90°.
3) треугольник ABC - равнобедренный => биссектриса, проведённая к основанию, является медианой => DC = 1/2 × AC = 1/2 × 25 = 12,5 см.
ответ: ∠В = 68°; ∠BDC = 90°; DC = 12,5 см.

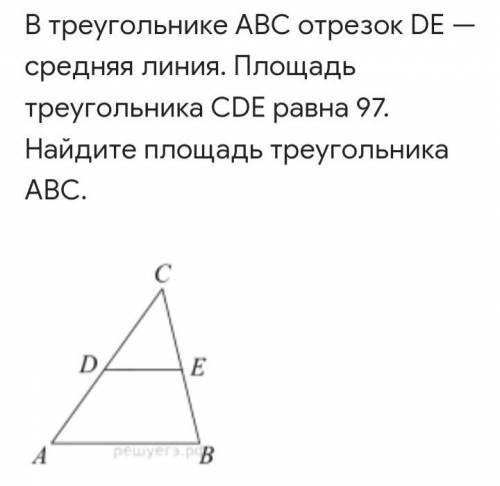
площадь треугольника в 8 раз больше потому что DE=1/2AB, CD= 1/2 CA, CE= 1/2 CB, все стороны в два раза больше потому что всё стороны в два раза больше 2*2*2=8 776
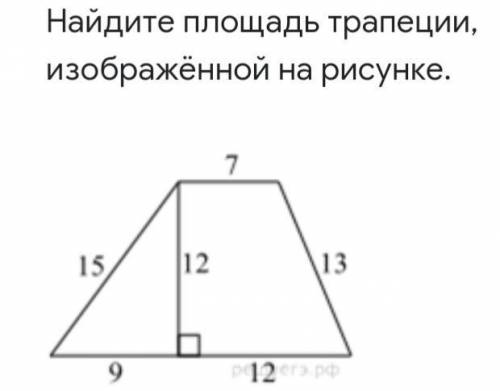
площадь трапеции= 7*12+9*12/2+13*5/2=84+54+32,5=170,5
Объяснение:
поставь коронку и