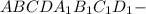 правильная четырехугольная призма
правильная четырехугольная призма
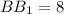 см
см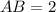 см
см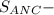 ?
?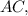 так как
так как 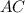 ⊂
⊂ 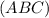 и
и 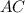 ⊂
⊂ 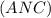
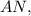 так как
так как 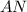 ⊂
⊂ 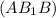 и
и 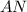 ⊂
⊂ 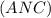
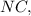 так как
так как  ⊂
⊂ 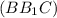 и
и  ⊂
⊂ 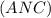
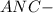 искомое сечение
искомое сечение 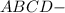 квадрат
квадрат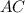 ∩
∩ 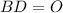
 см
см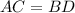 ( как диагонали квадрата)
( как диагонали квадрата)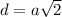
 см
см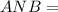 Δ
Δ 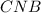 ( по двум катетам) ⇒
( по двум катетам) ⇒ 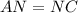
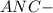 равнобедренный
равнобедренный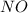 ⊥
⊥ 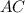
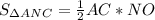
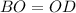
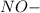 средняя линия Δ
средняя линия Δ 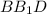
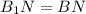 (по условию)
(по условию) 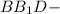 прямоугольный
прямоугольный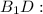
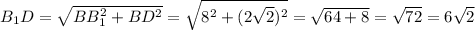 см
см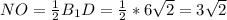 см
см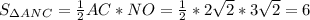 cм²
cм²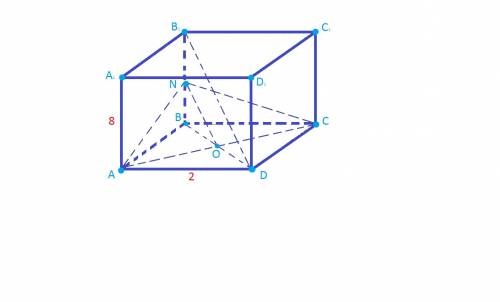
р - полупериметр ΔАВС,
r - радиус вписанной окружности.
AD = DB = 1/2 АВ = 4 см так как высота равнобедренного треугольника, проведенная к основанию, является медианой.
ΔACD: ∠ADC = 90°, по теореме Пифагора
AC = √(AD² + CD²) = √(16 + 9) = √25 = 5 см
p = (AC + CB + AB)/2 = (5 + 5 + 8)/2 = 9 см
Sabc = 1/2 AB · CD = 1/2 · 8 · 3 = 12 см²
r = S/p = 12 / 9 = 4/3 см
R = AB · AC · BC / (4Sabc) = 8 · 5 · 5 / (4 · 12) = 200 / 48 = 25/6 см