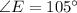
Проведём биссектрисы 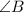 и
и 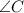 . Пусть они пересекаются в точке
. Пусть они пересекаются в точке 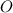 .
.
Также проведём отрезки 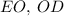 и
и 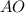 .
.
========================================
Рассмотрим 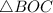 :
:
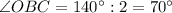 , т.к.
, т.к. 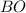 - биссектриса.
- биссектриса.
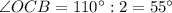 , т.к.
, т.к. 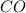 - биссектриса.
- биссектриса.
Сумма внутренних углов треугольника равна 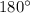 .
.
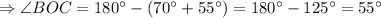
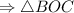 - равнобедренный.
- равнобедренный.
========================================
Рассмотрим 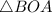 и
и 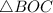 :
:
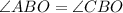 , т.к.
, т.к. 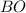 - биссектриса;
- биссектриса;
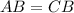 (по условию);
(по условию); 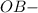 общая сторона.
общая сторона.
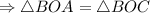 (по I признаку равенства треугольников).
(по I признаку равенства треугольников).
========================================
Рассмотрим 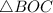 и
и 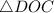 :
:
 , т.к.
, т.к. 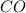 - биссектриса;
- биссектриса;
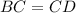 (по условию),
(по условию), 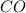 - общая сторона.
- общая сторона.
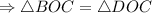 (по I признаку равенства треугольников).
(по I признаку равенства треугольников).
========================================
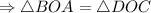 , т.е. мы имеем три равных равнобедренных тр-ка:
, т.е. мы имеем три равных равнобедренных тр-ка:
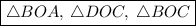
========================================
Рассмотрим 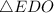 :
:
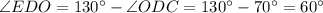 .
.
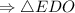 - равносторонний
- равносторонний 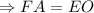
========================================
Рассмотрим геометрическую фигуру 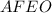 :
:
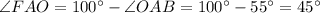 .
.
 (т.к. в полном угле всего 360°)
(т.к. в полном угле всего 360°)
При пересечении двух параллельных прямых секущей, сумма односторонних углов равна 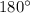 .
.
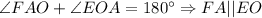
Если у геометрической фигуры есть 4 угла, 4 стороны, а 2 стороны равны и параллельны, то этот четырёхугольник - параллелограмм.
У параллелограмма противоположные углы равны.
 .
.
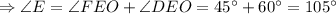
========================================
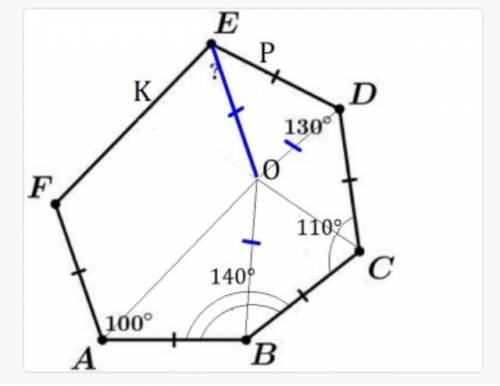
1). При пересечении прямых имеем 4 попарно равных угла в сумме =360°. Итак, у нас два угла по 30° и два угла по 150°
2). Угол ВСА = 180°-(36°+36°) = 72° = углу ВАС. Углы КАС и КАВ равны ( АК - биссектриса) =36°.
Треугольник САК - равнобедренный, т.к. углы КСА и АКС = 72°
Треугольник АКВ - равнобедренный, т.к. углы АВК и КАВ = 36°
3) Медиана делит сторону АС пополам. Соединяя любую точку на медиане с точками А и С имеем равные ртрезки АО и СО. У треугольников АОМ и СОМ равны стороны АМ и МС, АО и СО, а ОМ - общая, значит они равны.
4) В прямоугольном треугольнике АВС напротив угла 30° лежит катет, равный половине гипотенузы, то есть АС = 4.
АВ = АС²-ВС² = 2√3. Но АВ = 2АD*Cos30°; Cos30°= 0.866 (по таблице косинусов
АD = АВ/(2*0,866) = 2√3/(2*0,866) = 2 (т.к.√3= 2*0,866)
Итак, периметр АВС = АВ+ВС+СВ =2√3 +2+4 < 10.