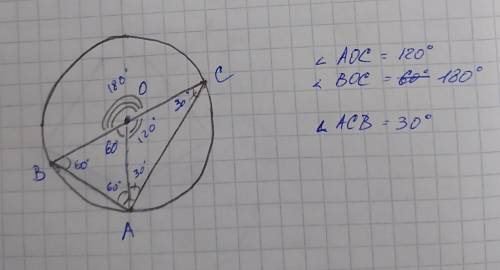
2. ∠AOC = 120°; ∠BOC = 180°; ∠ACB = 30°
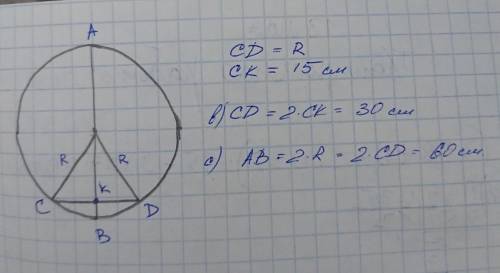
3. CD = 30 см; AB = 60 см
Объяснение:
2. Упростим соотношение дуг: 3:9:6 <=> 1:3:2 <=> AB, BC, AC
Найдём их градусную меру:
AB + BC + AC = x + 3x + 2x = 360°
6x = 360°
x = 60°
AB - 60°
BC - 180°
AC - 120°
Отразим это на рисунке.
Легко видеть, что
∠AOC = 120°; ∠BOC = 180°
На рисунке видно, что отрезок AO разделяет треугольник ABC на треугольник AOB и равнобедренный AOC. Поскольку сумма углов треугольника 180°, а угла у основания равнобедренного треугольика равны, то ∠ACB = (180° - 120°)/2 = 60°/2 = 30°
3. Рисунок и решение на фото.
ответ:Задание 1
Угол 31 градус и угол 2 равны между собой,как соответственные углы,следовательно,угол 2=31 градус
Углы 1 и 2-смежные,их сумма равна 180 градусов,мы знаем градусную меру угла 2, и можем узнать,чему равен угол1
180-31=149 градусов
Задание 2
Угол 131 градус и угол 2 являются накрест лежащими углами,накрест лежащие углы равны между собой,поэтому и угол 2=131 градус
Углы 1 и 2- смежные,их сумма равна 180 градусов,зная градусную меру угла 2 узнаём,чему равен угол 1
180-131=59 градусов
Объяснение:
угол АРВ = (дуга АВ + дуга СД)/2
Дуга АВ = центр. углу АОВ
Дуга СД = центр. углу СОД, значит
угол АРВ = (угол АОВ+угол СОД)/2
ч.т.д.