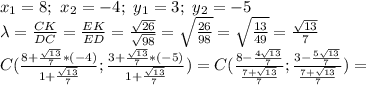
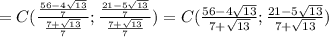
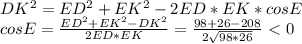
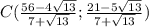
Вариант решения.
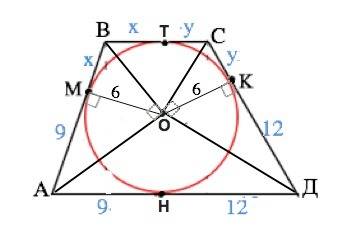
Обозначим трапецию АВСД, ВС и АД - основания.
Отрезки касательных к окружности, проведенных из одной точки, равны.⇒
АМ=АН=9, КД=ДН=12, ВМ=ВТ=х, СТ=СК=у
Соединим вершины трапеции с центром окружности.
Центр вписанной в угол окружности лежит на его биссектрисе.⇒ Центр вписанной в трапеции окружности лежит в точке пересечения биссектрис её углов.
Сумма углов при боковой стороне трапеции равна 180°, сумма их половин равна 90°, ⇒ ∆ АОВ и ∆ СОВ прямоугольные, радиусы ОМ и ОК– их высоты.
Высота прямоугольного треугольника - среднее пропорциональное между проекциями его катетов на гипотенузу.
ОМ²=АМ•ВМ
36=9•х⇒
х=36:9=4
Аналогично ОК²=ДК•СК
36=12•у
у=36:12=3
АВ=9+4=13
ВС=3+4=7
CD=12+3=15
АД=9+12=21
Площадь трапеции равна произведению высоты на полусумму оснований.
Высота описанной трапеции равна диаметру вписанной окружности
h=2r=12
S=(7+21)•12:2=168 ед. площади.
Объяснение:
Площадь параллелограмма равна произведению любой его стороны на высоту к этой стороне, поэтому
S =47,6*14=666,4 см^2