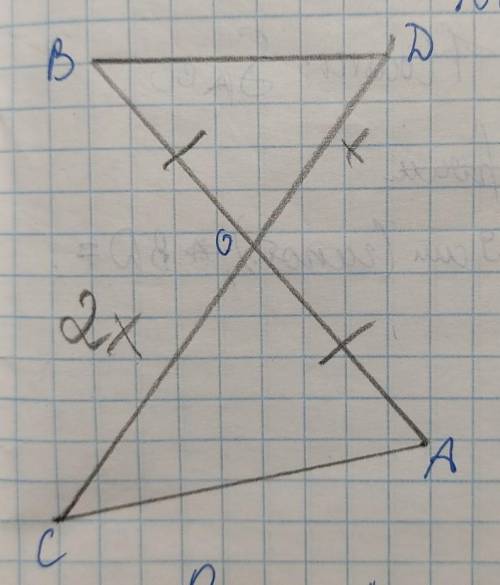
В доказательство ненужно ответа
Объяснение:
И так,чтобы AO было равно ОВ нужно доказать, что треугольники равны.
1) угол АОС = углу ДОБ(я просто с русского пишу), так как они вертикальные (свойство вертикальных углов)
2)Треугольники равны по двум углам и стороне между ними
3) Раз треугольники равны, следовательно
напротив равных углов лежат равные стороны, следовательно
AO лежит напротив угла С равного углу Д (по условию) напротив которого лежит сторона ОВ. Отсюда АО = ОВ и следовательно точка О центр сторон.
С другой стороны треугольники EBC и LDC подобны, поэтому EB/DL=BC/CD. Аналогично, треугольники BKC и DFC подобны, поэтому BK/FD=BC/CD. Значит EB/DL=BK/FD.
Перемножим полученные равенства EB/FD=BK/DL и EB/DL=BK/FD. Находим, что EB²/(FD·DL)=BK²/(DL·FD). После сокращения, EB²=BK², т.е. EB=BK. Отсюда и из равенства EB/FD=BK/DL следует, что и FD=DL.
Все подобия здесь по двум углам в силу парллельности прямых EK и FL.