25 см і 30 см
Объяснение:
Нехай ΔАВС - рівнобедрений, АВ = ВС, ∠ВАС < 60°. Бісектриса AD ділить висоту BЕ на відрізки BF = 27,5 см і FE = 16,5 см.
Знайти довжину відрізків BD та DC.
Розв'язання:
За властивістю бісектриси: АВ : АЕ = BF : FE = 27,5 : 16,5 = 5 : 3.
За теоремою Піфагора для ΔАВЕ:
AB² = AE² + BE²
(5x)² = (3x)² + (27,5 + 16,5)²
25х² = 9х² + 44²
16х² = 44²
(4х)² = 44²
4х = 44
х = 11
Отже, АВ = 5·11 = 55 см, АЕ = 3·11 = 33 см.
ВС = АВ = 55 см, АС = 2·АЕ = 33·2 = 66 см.
За властивістю бісектриси: ВD : DC = AB : AC = 55 : 66 = 5 : 6.
Нехай ВD = 5х, DC = 6х. Складемо рівняння:
BD + DC = BC
5х + 6х = 55
11х = 55
х = 5
ВD = 5·5 = 25 см
DC = 6·5 = 30 см
Составить уравнение окружности, если АВ - диаметр, А (4;8), В (-2;-4)
Объяснение:
Координаты центра О-середина АВ.
х(О)=
, у(О)=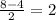 
. Получаем О( 1;2).
Найдем r=OA по формуле d=√( (х₁-х₂)²+(у₁-у₂)²), где (х₁;у₁), (х₂;у₂) -координаты концов отрезка.
r=√( (1-4)²+(2-8)²)=√(9+36)=√45.
Уравнение окружности (x – х₀)²+ (y – у₀)² = r² ,где (х₀; у₀)-координаты центра : (x – 1)²+ (y – 2)² =45