Объяснение:
Насколько я знаю, раньше считалось,что всего 4 океана,но сейчас их 5. Это Тихий, Атлантический, Индийский,Северно-Ледовитый и Южный(это как раз 5)
Уравнение окружности радиуса R с центром в точке C (a; b) имеет вид:
(x – a)² + (y – b)² = R².
1. Радиус — расстояние от центра окружности до любойточки на окружности. Таким образом, радиус будет равен расстоянию от точки c (2; 1) до точки d (5; 5).
Расстояние между точками A (x₁; y₁) и B (x₂; y₂) вычисляется по формуле:
AB = √((x₁ - x₂)² + (y₁ - y₂)²).
Таким образом, расстояние между точками c (2; 1) и d (5; 5) будет равно:
cd = R = √((2 - 5)² + (1 - 5)²) = √((- 3)² + (- 4)²) = √(9 + 16) = √25 = 5.
1. Подставим известные значения в уравнение окружности радиуса R = 5 с центром в точке c (2; 1):
(x – 2)² + (y – 1)² = 5²;
(x – 2)² + (y – 1)² = 25.
ответ: (x – 2)² + (y – 1)² = 25.
ответ: 26
Объяснение:
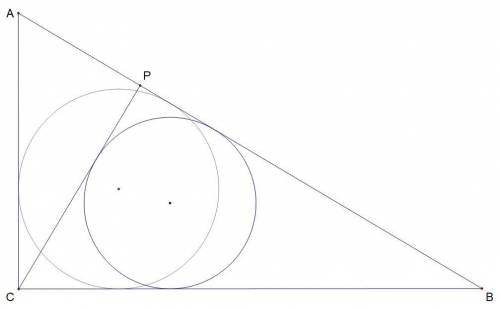
Пусть r -- радиус вписанной окружности в ΔBCP, а R -- радиус вписанной окружности в ΔBAC
1.
tg∠BAC = 12/5, откуда по определению тангенса
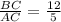
Пусть BC = 12x, тогда AC = 5x
По теореме Пифагора найдём AB:
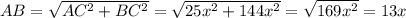
2.
tg∠CAP = 12/5, по определению тангенса из ΔACP
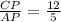
Пусть CP = 12y, тогда AP = 5y
Составим уравнение с теоремы Пифагора в ΔACP и выразим y через x:

Отрицательным y быть не может, так как он выражает длину отрезка, следовательно y = 5x/13, откуда
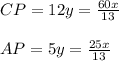
3. Выразим через x сторону BP, периметр и площадь ΔCPB:
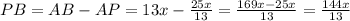
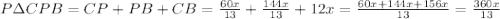
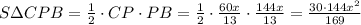
4. Используя формулу площади через радиус вписанной окружности составим уравнение:

5. Используя найденный x, вычислим периметр и площадь ΔABC:
PΔabc = AB + BC + AC = 13x + 12x + 5x = 30x = 30*13
SΔabc = 1/2 * AC * CB = 1/2 * 5x * 12x = 30x² = 30*13²
6. Найдём R, составив уравнение по формуле S = P/2 * R
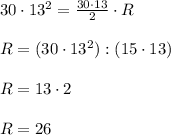
5 в мире вродебы 5 океанов
Объяснение:
я не могу обеснить это потому-что сам плохо знаю