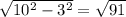. Значит, вся диагональ -- 
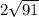, а сторона квадрата, которая в 
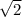раз меньше, чем диагональ, равна 
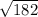. Таким образом, боковая грань представляет собой треугольник со сторонами 10, 10, 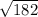. Площадь этого треугольника можно найти, например, опустив высоту из вершины, (эта высота будет и медианой). Получается, высота равна 
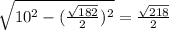, откуда площадь одного треугольника равна 
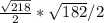, а площадь боковой поверхности равна площади четырёх таких треугольников, т. е. 
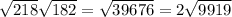Может, обсчитался где-то.
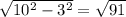. Значит, вся диагональ -- 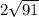, а сторона квадрата, которая в 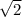раз меньше, чем диагональ, равна 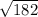. Таким образом, боковая грань представляет собой треугольник со сторонами 10, 10, 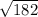. Площадь этого треугольника можно найти, например, опустив высоту из вершины, (эта высота будет и медианой). Получается, высота равна 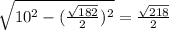, откуда площадь одного треугольника равна 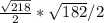, а площадь боковой поверхности равна площади четырёх таких треугольников, т. е. 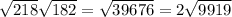Может, обсчитался где-то.
1)
S=a•b•sin α, где a и b -стороны, α - угол между ними.
sin d150°=0,5
S=6•10•0,5=30 (ед. площади)
2)
В параллелограмме сумма углов, прилежащих к одной стороне, равна 180°. (свойство углов при параллельных прямых и секущей).
Тогда острый угол параллелограмма равен 180°-150°=30°
Пусть дан параллелограмм АВСД. АВ=СД=6, ВС=АД=10
Тогда высота ВН, проведенная к АД, как катет прямоугольного треугольника АВН противолежит углу 30° и по свойству такого катета равна половине длины гипотенузы АВ.
ВН=6:2=3
S=a•h, где а - сторона, h- высота, проведенная к ней.
S=10•3=30 (ед. площади).