1. На данной прямой а отметим произвольную точку А.
2. Проведем окружность произвольного радиуса с центром в точке А. Точки пересечения окружности с прямой а обозначим В и С.
3. Проведем две окружности одинакового произвольного радиуса (большего половины отрезка ВС), с центрами в точках В и С.
4. Через точки пересечения этих окружностей (К и Н) проведем прямую b.
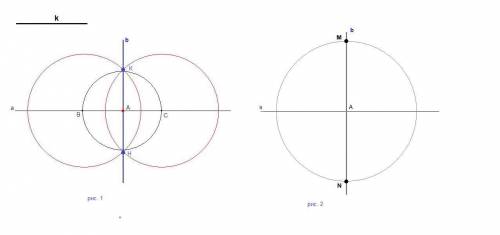
Прямая b - искомый перпендикуляр к прямой а. (см. рис. 1)
5. Проведем окружность с центром в точке А с радиусом, равным данному отрезку k. Точки пересечения этой окружности с прямой b обозначим M и N. (см. рис. 2)
Точки М и N - точки, удаленные от точки пересечения прямых на расстояние, равное длине данного отрезка.
Все построение надо выполнять, конечно, на одном чертеже. Для наглядности построение последнего пункта выполнено отдельно.
Уравнение окружности
(х-хо)² + (у-уо)²=R²
(хо; уо) - координаты центра окружности.
R - ее радиус.
У нас (х-1)² + (у-0)²=3²
Значит центр окружности т.О(1; 0) и радиус=3
Рисуем оси ОХ и ОУ.
Берем точку на оси ОХ: х=1; у=0 - это центр.
Циркулем с раствором=3 из этой точки проводим окружность.
Она пересечет ось ОХ в точках х=-2; х=4.
Масштаб берите любой. Можно 1 = 2 клеточки. Тогда радиус 6 клеток.