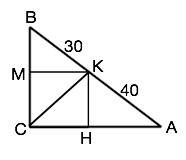
Все углы четырехугольника МКНС, вписанного в прямоугольный треугольник АВС – прямые, две стороны равны по условию, две другие им параллельны и противолежат, поэтому он – квадрат.
Его диагональ СМ для прямого угла С является биссектрисой.
Биссектриса угла треугольника делит противолежащую этому угла сторону на отрезки, пропорциональные прилежащим сторонам. ⇒
ВС:АС=ВК:АК.
Обозначим АС=х, ВС=у. ⇒
у:х=30:40 ⇒ у:х=3:4 ⇒
у=3х/4
АВ=30+40=7•10
По т.Пифагора
АВ²=АС²+ВС²=х²+у² Заменим у на его значение, выраженное через х:
7²•10²=х²+ 9х²/16
7²•10²=25x²/16
25x²=49•100•16
x²=49•4•16 ⇒x=7•2•4=56 см – длина АС
ВС=3•56/4=42 см
1. ответ
7+7+8=22
ну какбэ расстояние от одной вершины до точек касания сторон, выходящих из этой вершины с окружностью одинаково...
т.е. основание равно 4+4=8см
2.
ТК в треугольник вписана окружность, можно сделать подстановку. Касательны к окружности, проведённые из одной точки равны. ТОгда 1-ый катет равен (х+4), второй катет (у+4), т.к (у+х=26), то периметр равен
Р=(х+4)+(у+4)+26=х+у+8+26=60
3.Проведём из центра окружности к каждой вершине многоугольника отрезки, тем самым разбив многоугольник на треугольники.
Площадь треугольника равна половине произведения высоты треугольника на его основание.
Sтр = 1/2*h*L
Высота каждого треугольника в точности равна радиусу окружности, вследствие перпендикулярности радиуса и касательной.
h = r
Площадь многоугольника равна сумме площадей треугольников.
Sмн = Sтр1 + Sтр2 + Sтр3 + .
Sмн = 1/2*h*L1 + 1/2*h*L2 + 1/2*h*L3 + .
Вынесем 1/2*h за скобку.
Sмн = 1/2*h*(L1 + L2 + L3 + .)
Так как основания треугольников являются сторонами многоугольника, то сумма этих оснований равна периметру многоугольника.
L1 + L2 + L3 + .= P
Из этого получаем требуемое равенство.
Sмн = 1/2*h*P
Відповідь:
13,3 см
Пояснення:
радіус=10см, тоді діаметр буде=20см.Діаметр стягує дугу в 180°. а хорда 120° складемо пропорцію:20-180°
х-120° х=20*120/180=120/9=13,3 (см)