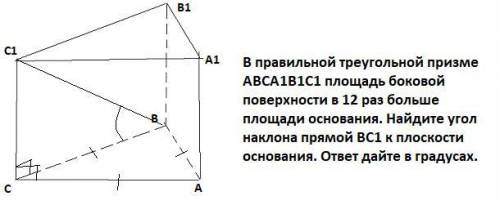
В правильной треугольной призме ABCA1B1C1 площадь боковой поверхности в 12 раз больше площади основания. Найдите угол наклона прямой BC1 к плоскости основания. ответ дайте в градусах.
Объяснение: S(бок)=12S(осн)
Т.к призма правильная , то СС₁⊥( АВС) и АВ=ВС=АС .
Углом наклона между прямой BC₁ к плоскости основания является угол между прямой и ее проекцией⇒∠С₁ВС.
Пусть сторона основания а , боковое ребро h. Тогда S(бок)=Р(осн)*СС₁=3аh , S(осн)=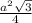 
3аh =12* 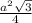⇒ h=a√3 .
ΔСВС₁- прямоугольный, tg(∠CBC₁)=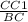 
, tg(∠CBC₁)= 
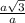, tg(∠CBC₁)=√3 , tg(∠CBC₁)=60°.
S(правильного треугольника)=(a^2)*корень из 3
a-сторона праильного треугольника
т.е a =корень из 12 = 2 корней из 3
Теперь если обозначчить этот треугольник, как ABC, то AB=BC=AC=2 корней из 3
O - центр описаного круга
Рассмотрим треугольник ABO:
AB= 2корней из 3
AO=BO=R(радиус описаной окружности)
Тогда ABO - равонбедренный, углы OAB и OBA по 30 градусов, а угол ABO 120 градусов
по теореме косинусов: AB^2=OA^2+OB^2-2OA*OB*cos 120
12=2R^2-2R^2*(-1/2)
12=2R^2+R^2
3R^2=12
R^2=4
R=2
l(Длина окружности)=2*Пи*R=2*2*Пи=4Пи